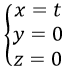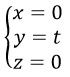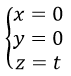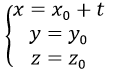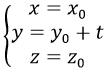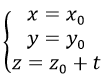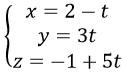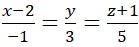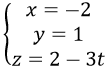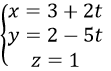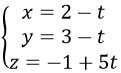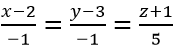Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) y = x3 + 3x2 + 1
Tập xác định: D = R
y’= 3x2 + 6x = 3x(x+ 2)
y’=0 ⇔ x = 0, x = -2
Bảng biến thiên:

Đồ thị hàm số:

b) Số nghiệm của phương trình \(x^3+3x^2+1=\dfrac{m}{2}\) chính là số giao điểm của (C) và đường thẳng (d): \(y=\dfrac{m}{2}\) (đường thẳng (d) vuông góc với Oy và cắt Oy tại \(\dfrac{m}{2}\) )
Từ đồ thị ta thấy:
- Với \(\dfrac{m}{2}< 1\Leftrightarrow m< 2\) : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
- Với \(\dfrac{m}{2}=1\Leftrightarrow m=2\) : (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm.
- Với \(1< \dfrac{m}{2}< 5\)\(\Leftrightarrow2< m< 10\)
- Với \(\dfrac{m}{2}=5\Leftrightarrow m=10\): (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.
- Với \(\dfrac{m}{2}>5\Leftrightarrow m>10\): (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
c) Điểm cực đại (-2, 5), điểm cực tiểu (0, 1).
Đường thẳng đi qua hai điểm này có phương trình là: 1\(y-14=x-2\Leftrightarrow y=x+12\).
a) y = x3 + 3x2 + 1
Tập xác định: D = R
y’= 3x2 + 6x = 3x(x+ 2)
y’=0 ⇔ x = 0, x = -2
Bảng biến thiên:

Đồ thị hàm số:

b) Số nghiệm của phương trình x^3+3x^2+1=m/2chính là số giao điểm của (C) và đường thẳng (d): y=m/2 (đường thẳng (d) vuông góc với Oy và cắt Oy tại )
Từ đồ thị ta thấy:
- Với m/2<1⇔m<2: (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
- Với m/2=1⇔ m = 2: (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm
- Với 1<m/2<5⇔ 2<m
- Với m/2=5⇔m=10: (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.
- Với m/2>5⇔m>10 : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
c) Điểm cực đại (-2, 5), điểm cực tiểu (0, 1).
Đường thẳng đi qua hai điểm này có phương trình là: y−14=x−2⇔y=−2x+1

a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
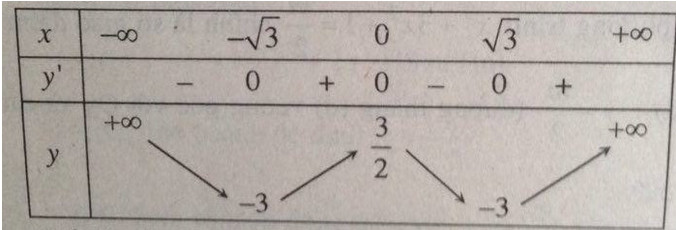
Đồ thị hàm số:
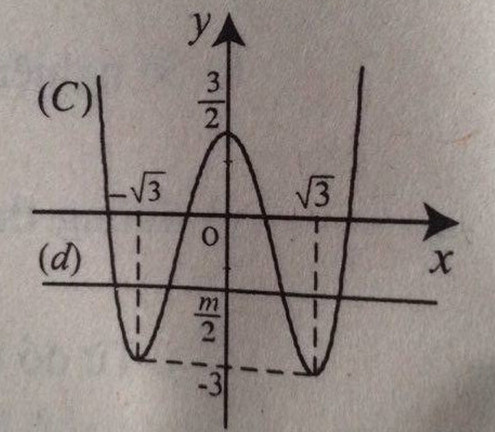
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm

Ta có: \(f\left(x\right)=y=\frac{x^2+mx}{1-x}\Rightarrow y'=\frac{\left(2x+mx\right)\left(1-x\right)+\left(x^2+mx\right)}{\left(1-x\right)^2}=\frac{-x^2+2x+m}{\left(1-x\right)^2}\)\(\)\(\left(D=R/\left\{1\right\}\right)\)
Đặt \(g\left(x\right)=-x^2+2x+m\)\(\Rightarrow\)f(x) cùng dấu với y' trên D
Xét pt g(x)=0
\(\Delta'=m+1\), Hàm số có 2 điểm cực trì<=> pt có 2 nghiệm phân biệt khác 1
\(\Leftrightarrow\hept{\begin{cases}\Delta'>0\\f\left(1\right)\ne0\end{cases}\Leftrightarrow m>-1}\)
Khi đó 2 điểm cực trì là A(x1,f(x1) ) và B(x2, f(x2) )
Lại có \(f'\left(x_1\right)=\frac{\left(2x_1+m\right)\left(1-x_1\right)+\left(x_1^2+mx_1\right)}{\left(1-x_1\right)^2}=0\Rightarrow x_1^2+mx_1=-\left(2x_1+m\right)\left(1-x_1\right)\)
\(\Rightarrow f\left(x_1\right)=\frac{x_1^2+mx_1}{1-x_1}=-2x_1-m.\)
=>\(f\left(x_2\right)=-2x_2-m\)
Khoảng cách giữa 2 điểm cực trị:
\(AB=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}=\sqrt{\left(x_1-x_2\right)^2+\left(2x_1-2x_2\right)^2}=|x_1-x_2|\sqrt{5}=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=20\)
A/d Vi-ét cho pt g(x)=0\(\Rightarrow4+4m=20\Leftrightarrow m=4\)
Vậy m=4

a) Điểm (-1 ; 1) thuộc đồ thị của hàm số ⇔ .
b) m = 1 . Tập xác định : R.
y' = 0 ⇔ x = 0.
Bảng biến thiên:
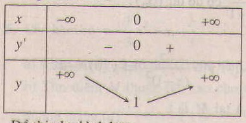
Đồ thị như hình bên.
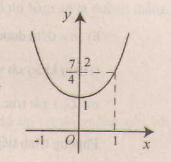
c) Vậy hai điểm thuộc (C) có tung độ
là A(1 ;
) và B(-1 ;
). Ta có y'(-1) = -2, y'(1) = 2.
Phương trình tiếp tuyến với (C) tại A là : y - = y'(1)(x - 1) ⇔ y = 2x -
Phương trình tiếp tuyến với (C) tại B là : y - = y'(-1)(x + 1) ⇔ y = -2x -
.

vecto chỉ phương của d là a = PQ = (4;2;1) (vì d đi qua hai điểm P(1;2;3),Q(5;4;4)
Vậy pt tham số của đường thẳng d là: x = 1 + 4 t y = 2 + 2 t z = 3 + t

a) Tập xác định : D = R
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
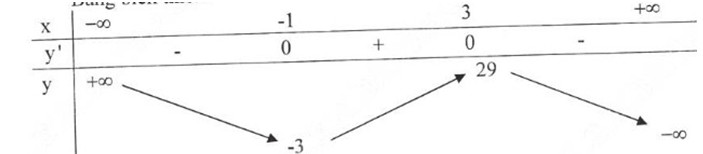
Đồ thị hàm số:
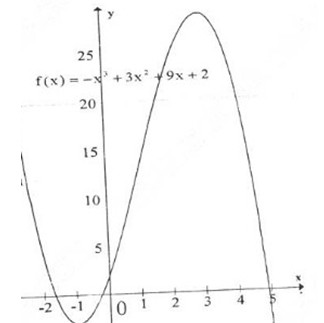
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6

\(y'=4x\left(x-m\right)\left(x+m\right)\\ y'=0\Leftrightarrow\begin{cases}x=0\\x=\pm m\end{cases}\)
Với m=0 thì hàm số có 3 cực trị là 0, -m và m
đồ thị hàm số có 3 điểm cực trị \(A\left(0;1\right),M\left(-m;1-m^4\right),N\left(m;1-m^4\right)\)
Nhận thấy \(AM=AN\) nên \(\Delta AMN\) cân tại A với mọi m
Gọi trung điểm MN là \(I\left(0;1-m^4\right)\)
\(\Delta AMN\) vuông cân tại A khi và chỉ khi \(IA=IM=IN\) hay\(IA=IN\)
\(\Leftrightarrow IA=IN\Leftrightarrow\left|m^4\right|=\left|m\right|\Leftrightarrow m=\pm1\) (vì \(m\ne0\))

a) Trục Ox là đường thẳng đi qua O(0, 0, 0) và nhận i→=(1,0,0) làm vectơ chỉ phương nên có phương trình tham số là:
* Tương tự, trục Oy có phương trình
Trục Oz có phương trình
b) Đường thẳng đi qua M0 (x0,y0,z0) song song với trục Ox sẽ có vectơ chỉ phương là i→(1,0,0) nên có phương trình tham số là:
tương tự ta có Phương trình của đường thẳng đi qua M0 (x0,y0,z0) và song song với Oy là:
phương trình đường thẳng đi qua M0 (x0,y0,z0) và song song với Oz là
c) Đường thẳng đi qua M(2, 0, -1) và có vectơ chỉ phương u→(-1,3,5) có phương trình tham số là
có phương trình chính tắc là
d) Đường thẳng đi qua N(-2, 1, 2) và có vectơ chỉ phương u→(0,0,-3) có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
e) Đường thẳng đi qua N(3, 2, 1) và vuông góc với mặt phẳng: 2x- 5y + 4= 0 nên nó nhận vectơ pháp tuyến của mặt phẳng này làn→(2,-5,0) là vectơ chỉ phương, nên ta có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
f) Đường thẳng đi qau P(2, 3, -1) và Q(1, 2, 4) sẽ nhận PQ→(-1,-1,5) là vectơ chỉ phương, nên có phương trình tham số là
và có phương tình chính tắc là