Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khi a = 0 ta có hàm số: y=−13x3−x2+3x−4y=−13x3−x2+3x−4
- Tập xác định : (-∞, +∞)
- Sự biến thiên: y’= -x2 – 2x + 3
y’=0 ⇔ x = 1, x = -3
Trên các khoảng (-∞, -3) và (1, +∞), y’ < 0 nên hàm số nghịch biến.
Trên khoảng (-3, 1), y’ > 0
_ Cực trị:
Hàm số đạt cực đại tại x = 1, yCD=−73yCD=−73
Hàm số đạt cực tiểu tại x = -3, yCT=−13yCT=−13
_ giới hạn vô cực : limx→+∞=−∞,limx→−∞=+∞limx→+∞=−∞,limx→−∞=+∞
Bảng biến thiên:
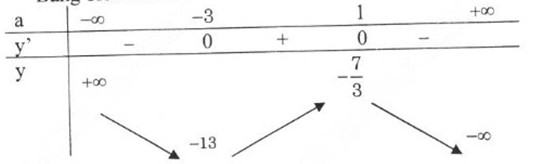
Đồ thị hàm số:
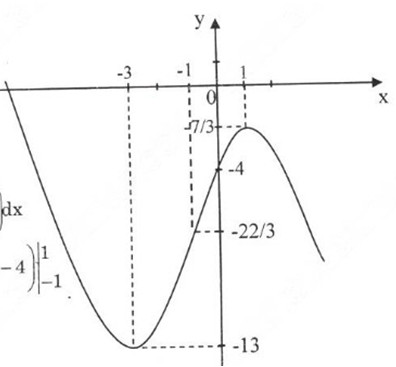
Đồ thị cắt trục tung tại y = -4
Đồ thị cắt trục hoành tại x ≈ 5, 18
b) Hàm số y=−13x3−x2+3x−4y=−13x3−x2+3x−4 đồng biến trên khoảng (-3, 1) nên:
y < y(1) = −73−73 < 0, ∀x ∈ (-1, 1)
Do đó , diện tích cần tính là:
∫1−1(−13x3−x2+3x−4)dx=263
Xem thêm tại: http://loigiaihay.com/cau-2-trang-145-sgk-giai-tich-12-c47a26419.html#ixzz4czxQ4IGx



nên từ đồ thị (C) ta suy ra ngay đồ thị của hàm số :
\(y=\left|\dfrac{x^3}{6}+\dfrac{3x^2}{2}+\dfrac{5x}{2}\right|\) là hình 18