Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

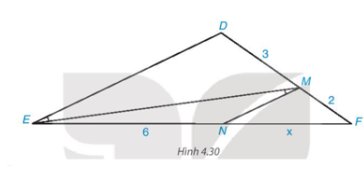
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)


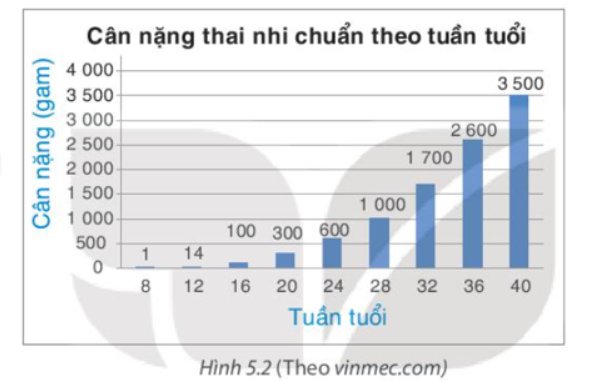
Từ biểu đồ trên, ta lập bảng thống kê:
Tuần tuổi | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
Cân nặng (gam) | 1 | 14 | 100 | 300 | 600 | 1 000 | 1 700 | 2 600 | 3 500 |
Ta có thể dùng biểu đồ đoạn thẳng để biểu diễn dữ liệu trên.

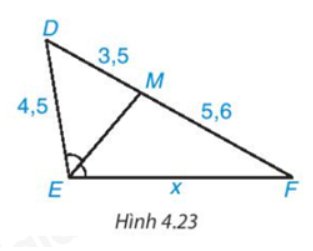
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

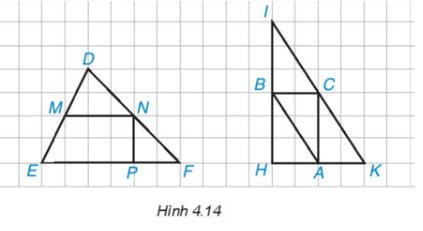
Đường trung bình trong tam giác DEF là: cạnh MN.
Đường trung bình trong tam giác HIK là: cạnh BC, CA, AB.
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.






Thời gian đội đi xuôi dòng từ A đến B là: \(\dfrac{3}{{x + 1}}\) (giờ)
Thời gian đội đi ngược dòng từ B về A là: \(\dfrac{3}{{x - 1}}\) (giờ)
Điều kiện: \(x \ne \pm 1\)
Thời gian thi của đội là:
\(\dfrac{3}{{x + 1}} + \dfrac{3}{{x - 1}} = \dfrac{{3\left( {x - 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} + \dfrac{{3\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \dfrac{{3x - 3 + 3x + 3}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \dfrac{{6x}}{{{x^2} - 1}}\) (giờ)
Chênh lệch giữa thời gian đi và bề của đội là: \(\dfrac{3}{{x - 1}} - \dfrac{3}{{x + 1}} = \dfrac{{3\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \dfrac{{3\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \dfrac{{3x + 3 - 3x + 3}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \dfrac{6}{{{x^2} - 1}}\) (giờ)
Khi \(x = 6\) (thỏa mãn điều kiện) thì thời gian thi của đội là: \(\dfrac{{6.6}}{{{6^2} - 1}} = \dfrac{{36}}{{36 - 1}} = \dfrac{{36}}{{35}}\) (giờ)
Khi \(x = 6\) (thỏa mãn điều kiện) thì chênh lệch giữa thời gian đi và về của đội là: \(\dfrac{6}{{{6^2} - 1}} = \dfrac{6}{{36 - 1}} = \dfrac{6}{{35}}\) (giờ)