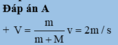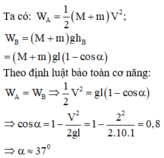Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
P1 =m1g => m1 = 1(kg)
P2 = m2g => m2 =1,5(kg)
Trước khi nổ, hai mảnh của quả lựu đạn đều chuyển động với vận tốc v0, nên hệ vật có tổng động lượng : \(p_0=\left(m_1+m_2\right)v_0\)
Theo đl bảo toàn động lượng : \(p=p_0\Leftrightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v_0\)
=> \(v_1=\frac{\left(m_1+m_2\right)v_0-m_2v_2}{m_1}=\frac{\left(1+1,5\right).10-1,5.25}{1}=-12,5\left(m/s\right)\)
=> vận tốc v1 của mảnh nhỏ ngược hướng với vận tốc ban đầu v0 của quả lựu đạn.
Bài2;
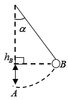
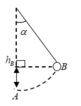
Vận tốc mảnh nhỏ trước khi nổ là :
v02=\(v_1^2=2gh\)
=> v1 = \(\sqrt{v_0^2-2gh}=\sqrt{100^2-2.10.125}=50\sqrt{3}\left(m/s\right)\)
Theo định luật bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
p = mv = 5.50 =250(kg.m/s)
\(\left\{{}\begin{matrix}p_1=m_1v_1=2.50\sqrt{3}=100\sqrt{3}\left(kg.m/s\right)\\p_2=m_2v_2=3.v_2\left(kg.m/s\right)\end{matrix}\right.\)
+ Vì \(\overrightarrow{v_1}\perp\overrightarrow{v_2}\rightarrow\overrightarrow{p_1}\perp\overrightarrow{p_2}\)
=> p2 = \(\sqrt{p_1^2+p^2}=\sqrt{\left(100\sqrt{3}\right)^2+250^2}=50\sqrt{37}\left(kg.m/s\right)\)
=> v2= \(\frac{p_2}{m_2}=\frac{50\sqrt{37}}{3}\approx101,4m/s+sin\alpha=\frac{p_1}{p_2}=\frac{100\sqrt{3}}{50\sqrt{3}}\)
=> \(\alpha=34,72^o\)

Vì chỉ có 2 vật tương tác vs nhau nên động năng đc bảo toàn
Chọn chiều dương là chiều chuyển động của vật A trước khi va chạm
Động năng của hệ trước khi va chạm là:
\(W_{đ1}=\frac{1}{2}m_A.v_{A1}^2=\frac{1}{2}.m_A.1^2=\frac{1}{2}m_A\left(J\right)\)
Động năng của hệ sau va chạm
\(W_{đ2}=-\frac{1}{2}m_A.v_A^2+\frac{1}{2}m_B.v_B^2\left(J\right)\)
ĐLBTĐN:
\(\frac{1}{2}m_A=-\frac{1}{2}m_A.v_A^2+\frac{1}{2}m_B.v_B^2\)
\(\Leftrightarrow\frac{1}{2}m_A=-\frac{1}{2}.m_A.0,1^2+\frac{1}{2}.0,2.0,55^2\)
\(\Leftrightarrow1,01m_A=0,0605\Leftrightarrow m_A=0,06\left(kg\right)=600\left(g\right)\)