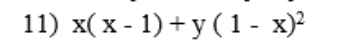Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4,\(6x^2+10x-9x-15=6x^2+12x\)
\(6x^2+x-15-6x^2-12x\) =0
11x-15=0
11x=15
x=\(\frac{15}{11}\)
vậy.......
hc tốt
\(a,\left(2x-3\right)\left(3x+5\right)+3=6x\left(x+2\right)\)
\(\Rightarrow6x^2+2x-15+3=6x^2+12x\)
\(\Rightarrow10x=-12\)
\(\Rightarrow x=-\frac{5}{7}\)
\(b,\)Sai đề không ?

- Nhân đơn thức với đa thức: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
- Nhân đa thức với đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

- quy tắc nhân đơn thức với đa thức:Muốn nhân một đơn thức với một đa thức ta nhân đơn thức với từng số hạng của đa thức rồi cộng các tích với nhau.
- quy tắc nhân đa thức với đa thức:Muốn nhân một đa thưc với một đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Quy tắc nhân đơn thức với đa thức:
Muốn nhân một đơn thức với một đa thức ta nhân đơn thức với từng số hạng của đa thức rồi cộng các tích với nhau.
Công thức:
Cho A, B, C, D là các đơn thức, ta có: A(B + C - D) = AB + AC - AD.
2. Nhắc lại các phép tính về lũy thừa:
an = a . a . a … a (a ∈ Q, n ∈ N*)
a0 = 1 (a ≠ 0)
an . am = an + m
an : am = an – m (n ≥ m)
(am)n = am . n

Quy tắc nhân đơn thức với đa thức:
Muốn nhân một đơn thức với một đa thức ta nhân đơn thức với từng số hạng của đa thức rồi cộng các tích với nhau.
Muốn nhân một đa thức với một đa thức
Qui tắc: Muốn nhân một đa thức với một đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
- Quy tắc nhân đơn thức với đa thức:
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng tích với nhau
- Quy tắc nhân đa thức với đa thức:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng tích với nhau

\(5,\)\(\frac{1}{5}x\left(10x-15\right)-2x\left(x-5\right)+7x\)
\(=2x^2-3x+-2x^2+10x-7x\)
\(=0\)
\(\Rightarrow\)Giá trị biểu thức không phụ thuộc vào biến x
\(6,\)\(F=5\left(x^2-3x\right)-x\left(3-5x\right)+18x+3\)
\(=5x^2-15x-3x-5x^2+18x+3\)
\(=3\)
Vậy giá trị biểu thức không phụ thuộc vào biến x
( À có một số chỗ mình phải sửa đề mới đúng đó. Cậu coi lại giùm mình nha )

\(=x\left(x-1\right)+y\left(x-1\right)^2=\left(x-1\right)\left[x+y\left(x-1\right)\right]\\ =\left(x-1\right)\left(x+xy-y\right)\)

Đơn thức là: x2 và đa thức là: x2 + x + 1
Ta có:
x2.(x2 + x + 1) = x2.x2 + x2.x + x2.1
= x(2 + 2) + x(2 + 1) + x2
= x4 + x3 + x2
Khi đó: đa thức x4 + x3 + x2 là tích của đơn thức x2 và x2 + x + 1

Câu 1:
Nhân từng hạng tử của đa thức/đơn thức này cho từng hạng tử của đa thức/đơn thức kia. Sau đó, thu gọn lại ta được kết quả cần tìm
Câu 2:
Có 7 hằng đẳng thức. Công thức:
1: \(\left(a+b\right)^2=a^2+2ab+b^2\)
2: \(\left(a-b\right)^2=a^2-2ab+b^2\)
3: \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
4: \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
5: \(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
6: \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
7: \(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)

\(x^4+2008x^2+2007x+2008\\ =x^4-x+2008\left(x^2+x+1\right)=x\left(x^3-1\right)+2008\left(x^2+x+1\right)=x\left(x-1\right)\left(x^2+x+1\right)+2008\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left(x^2-x+2008\right)\)
Ta có: \(x^4+2008x^2+2007x+2008\)
\(=x^4-x+2008\left(x^2+x+1\right)\)
\(=x\left(x^3-1\right)+2008\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x^2+x+1\right)+2008\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^2-x+2008\right)\)