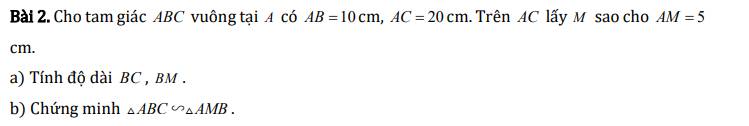K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 8
a: ta có: EI⊥BF
AC⊥BF
Do đó: EI//AC
=>\(\hat{IEB}=\hat{ACB}\) (hai góc đồng vị)
mà \(\hat{ABC}=\hat{ACB}\) (ΔABC cân tại A)
nên \(\hat{KBE}=\hat{IEB}\)
Xét ΔKBE vuông tại K và ΔIEB vuông tại I có
BE chung
\(\hat{KBE}=\hat{IEB}\)
Do đó: ΔKBE=ΔIEB
=>EK=BI
b: Điểm D ở đâu vậy bạn?
LN
5
15 tháng 8
bạn lưu ảnh rồi gửi qua file đi ạ chứ bn cóp sang thì ko hiện ảnh mất rồi
LN
1
13 tháng 8
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\frac{BC}{2}=\frac{12}{2}=6\left(\operatorname{cm}\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=100-36=64=8^2\)
=>HA=8(cm)
b: Diện tích tam giác ABC là:
\(S_{ABC}=\frac12\cdot AH\cdot BC=\frac12\cdot12\cdot8=4\cdot12=48\left(\operatorname{cm}^2\right)\)
LN
5
LN
3
S
subjects
CTVHS
13 tháng 8
a. áp dụnng định lý pythagore vào △ ABC vuông tại A ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(\operatorname{cm}\right)\)
b. diện tích △ ABC là:
\(\frac{6\cdot8}{2}=24\left(\operatorname{cm}^2\right)\)
c. ta có: \(BC\cdot AH=AB\cdot AC\)
\(\Rightarrow AH=\frac{AB\cdot AC}{BC}=\frac{6\cdot8}{10}=4,8\left(\operatorname{cm}\right)\)
áp dụng định lý pythagore vào △ ABH vuông tại H ta được:
\(HB=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6\left(\operatorname{cm}\right)\)
áp dụng định lý pythagore vào △ AHC vuông tại H ta được:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=6,4\left(\operatorname{cm}\right)\)
d. vì M là trung điểm của cạnh BC
⇒ MB = MC = BC : 2 = 10 : 2 = 5 (cm)
ta có: BH + HM = BM
⇒ HM = BM - BH = 5 - 3,6 = 1,4 (cm)
áp dụng định lý pythagore vào △ AHM vuông tại H ta có:
\(AM=\sqrt{AH^2+HM^2}=\sqrt{4,8^2+1,4^2}=5\left(\operatorname{cm}\right)\)
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
P
Phong
CTVHS
23 tháng 1 2024
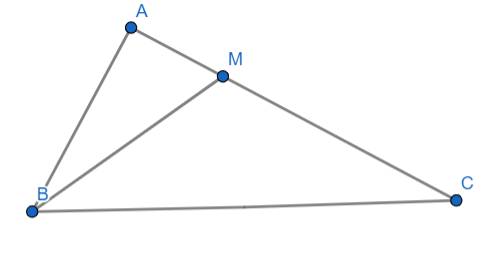
a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABM vuông tại A ta có:
\(BM^2=AB^2+AM^2\)
\(\Rightarrow BM=\sqrt{AB^2+AM^2}\)
\(\Rightarrow BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b) Ta có:
\(\dfrac{AM}{AB}=\dfrac{1}{2}\)
\(\dfrac{BM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
Xét hai tam giác ABC và AMB có:
\(\widehat{BAC}\) chung
\(\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta AMB\left(c.g.c\right)\)
