PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
22 tháng 9 2019
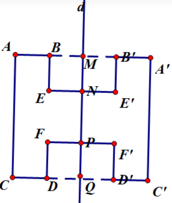
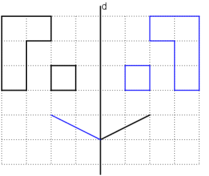
- Kéo dài AB, CD cắt d tại M, Q
- Trên tia AB lấy A', B' sao cho MB' = MB; MA' = MA
- Trên tia CD lấy C', D' sao cho QC' = QC; QD' = QD
- Trên tia EN lấy E' sao cho NE = NE'
- Trên tia FP lấy F' sao cho PF = PF'
Nối các điểm đã dựng ta được hình đối xứng qua d của hình đã cho.
SG
1
CM
6 tháng 4 2019
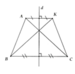
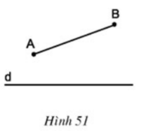
a) Đoạn thẳng đối xứng với AB, AC qua đường thẳng d lần lượt là KC, KB.
b) ta có AK//BC (vì cùng vuông góc với d) và AC = KB (tính chất đối xứng trục) Þ tứ giác AKCB là hình thang cân
22 tháng 10 2023
a: Xét tứ giác ADHE có
AD//HE
AE//HD
Do đó: ADHE là hình bình hành
b: AE=HD(ADHE là hình bình hành)
DM=DH
Do đó: AE=DM
Xét tứ giác AEDM có
AE//DM
AE=DM
Do đó: AEDM là hình bình hành
c: Đề sai rồi bạn
PT
1
C
28 tháng 4 2017
a) Đxứng với AB qua d là KC, AC qua d là KB
b) Ta có: d là trung trực nên
AK\(\perp d;BC\perp d\)
hay AK//BC
=> AKCB là hình thang
lại có AC= KB ( AC đx với KB qua d)
=> hình thang AKCB là hình thang cân
28 tháng 4 2017
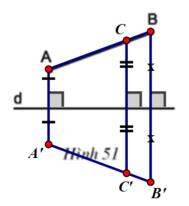
a, Đoạn thẳng đối xứng với đoạn thẳng AB qua d là KC
Đoạn thẳng đối xứng với đoạn thẳng AC qua d là KB
b, Vì d là đường trung trực của AK và BC nên AK vuông góc với d và BC vuông góc với d. Vậy AK//BC, do đó AKCB là hình thang.
Theo câu a) AC đối xứng với KB qua d, do đó AC=KB. Hình thang AKCB có 2 đường chéo bằng nhau nên là hình thang cân
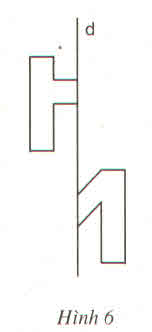
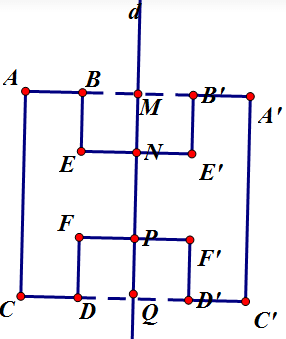
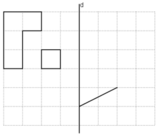
- Giả sử AB ∩ d = I; CD ∩ d = H
- Trên tia AB lấy A', B'sao cho IA = IA'; IB = IB'
- Trên tia CD lấy C', D' sao cho HC' = HC; HD' = HD
- Từ E kẻ đường vuông góc với d, cắt d tại J
- Trên EJ lấy E' sao cho JE = JE'
Nối các điểm đã dựng ta được hình đối xứng qua d của hình đã cho.