Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

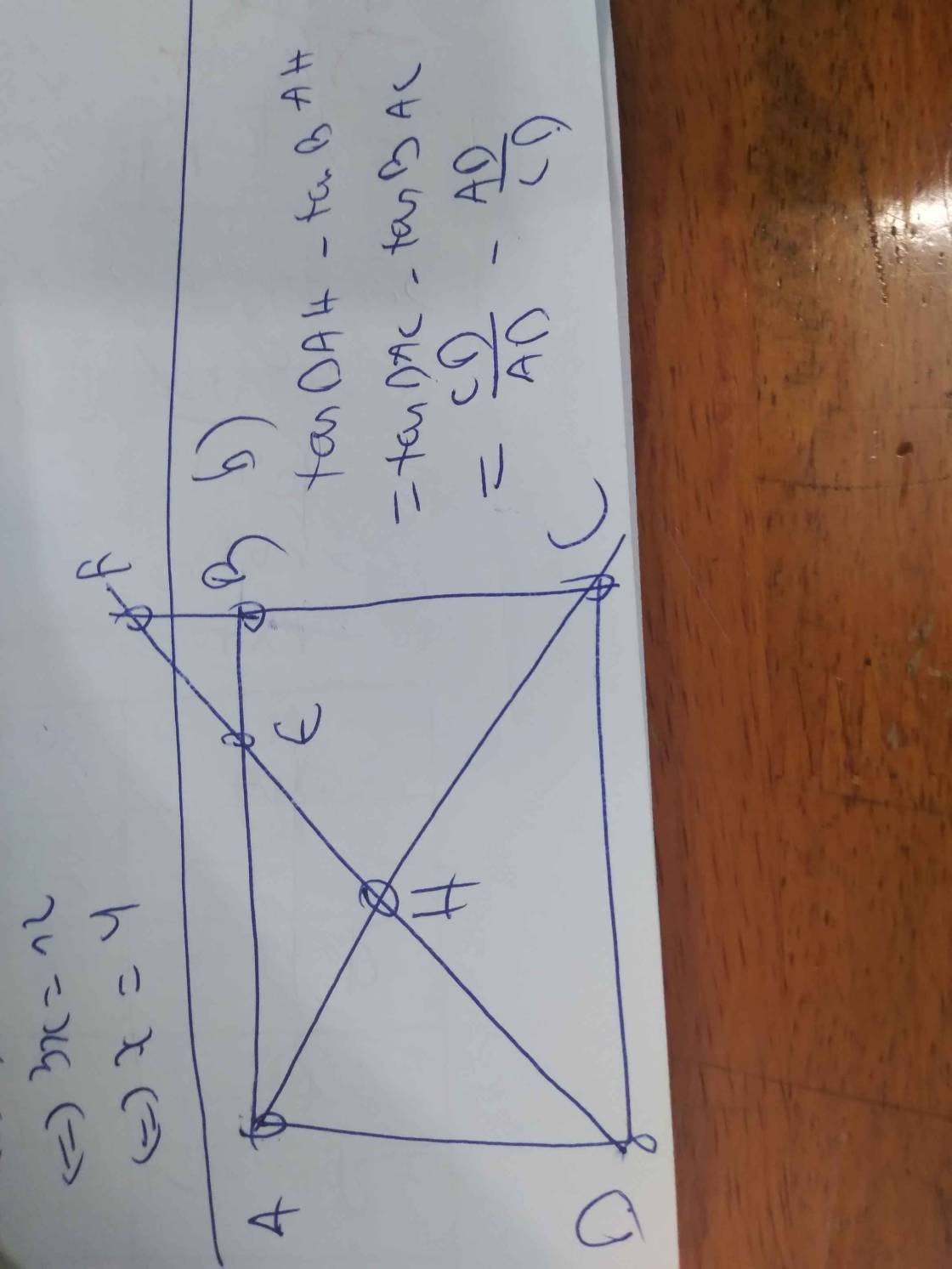
a) ta có ap//bc nên ae/ec=ep/eb
ta có ab//cq nên ae/ec=be/eq
vậy ep/eb=be/eq nên eb^2=ep.eq
ap//bc nên ap/bc=ae/ec
nên ab/cq=ap/bc
vậy ap.cq=ab.bc ko đổi
làm cho những người sau có thể bt mà xem

a, AC = 36:3,6=10 (cm)
AB2 = 102-62= 64 , AB = 8 (cm)
a/ dùng hệ thức lượng :
AC = 10cm
AB = 8cm
b/ AB2 - AD2 = CD2 - AD2 = DH.DF - DH.DE = DH(DF - DE) = DH.EF

Kẻ BK // AC => BK vuông vs BD (vì AC vuông vs BD)
=> ABKC là hình bình hành
=> AB = CK = 18cn
=> DK = DC + CK = 32 + 18 = 50cm
Có: BD2 = DK2 - BK2
BD2 = AD2 + AB2
=> DK2 - BK2 = AD2 + AB2
=> 502 - AC2 = AD2 + 182
=> AD2 + AC2 = 502 - 182 = 2176 (1)
Có: AC2 - AD2 = DC2 = 322 = 1024 (2)
Từ (1) và (2) ta có hệ pt => AC2 = 1600 => AC = 40cm
Vậy AC = 40cm

Cho 3 số thực dương a;b;c thỏa mãn : a+ b + c = 1 . CMR
\(\frac{a+1}{a+b+c}+\frac{b+1}{b+ac}+\frac{c+1}{c+ab}\ge9\)Dấu " = " xay ra khi nào

a/ Ta có CF vuông góc AB tại F (gt)
Nên góc CFB = 90 độ
BE vuông góc AC tại E
Nên góc BEC = 90 độ
Tứ giác CEFB có hai đỉnh kề F và E cùng nhìn cạnh BC dưới một góc vuông . Do đó tứ giác CEFB nt
Ta có góc BFC = 90(cmt) độ nên tam giác BFC vuông tại F .
góc BEC = 90 độ (cmt)
Nên tam giác BEC vuông tại E
Tam giác vuông BFC và BEC đều có BC là cạnh huyền nên tâm của đường tròn ngoại tiếp tứ giác là trung điểm của cạnh BC .