Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Góc xOy và góc x’Oy’ là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox’ và cạnh Oy là tia đối của cạnh Oy’
b) Góc y’Ox và góc yOx’ là hai góc đối đỉnh vì cạnh Oy’ là tia đối của cạnh Oy và cạnh Ox là tia đối của cạnh Ox’

1. x O x' y y'
Giải: a) Ta có: \(\widehat{xOy}+\widehat{yOx'}=180^0\) (kề bù)
=> \(\widehat{yOx'}=180^0-\widehat{xOy}=180^0-75^0=105^0\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOy}=75^0\) => \(\widehat{x'Oy'}=75^0\)
\(\widehat{yOx'}=\widehat{xOy'}\) (đối đỉnh)
Mà \(\widehat{yOx'}=105^0\) => \(\widehat{xOy'}=105^0\)
1b) Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
mà \(\widehat{x'Oy}-\widehat{xOy}=30^0\)
=> \(2.\widehat{x'Oy}=210^0\)
=> \(\widehat{x'Oy}=210^0:2=105^0\) => \(\widehat{x'Oy}=\widehat{xOy'}=105^0\) (đối đỉnh)
=> \(\widehat{xOy}=180^0-105^0=75^0\) => \(\widehat{xOy}=\widehat{x'Oy'}=75^0\) (đối đỉnh)
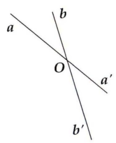
2. O x y x' y' m m'
Giải: a) Ta có: \(\widehat{xOm}=\widehat{x'Om'}\) (đối đỉnh)
\(\widehat{mOy}=\widehat{m'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}\) (gt)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}.\widehat{xOy}\) (vì Om là tia p/giác)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}=\frac{1}{2}.\widehat{xOy}\)
=> Om' nằm giữa Ox' và Oy'
=> Om' là tia p/giác của góc x'Oy'
b) Tự viết

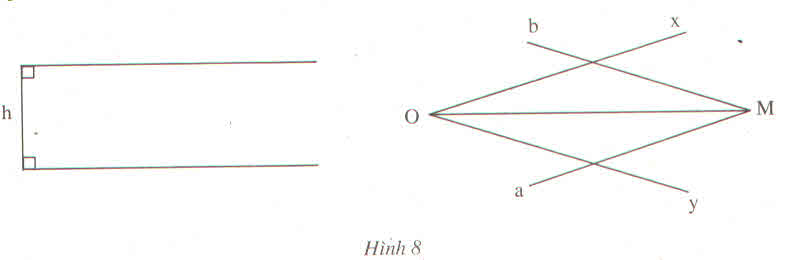
Kẻ MH vuông góc với Ox, MK vuông góc với Oy
=>MH và MK là chiều rộng của thước hai lề
=>MH=MK
=>M thuộc tia phân giác của góc xOy
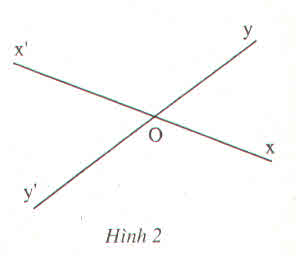
a) Góc xOy và góc .....là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
ghi ngắn gọn là ( ghi mỗi đáp án)
a) X'OY'
b) là hai góc đối đỉnh
+) Của cạnh OX' và cạnh OY là tia đối của cạnh OY'