
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)


=> ΔΔBCE vuông tại E => HC=BC2CE=BC22ACHC=BC2CE=BC22AC
AH=AC−HC=AC−BC22AC=2AC2−BC22ACAH=AC−HC=AC−BC22AC=2AC2−BC22AC
⇒AHHC=2(ACBC)2−1

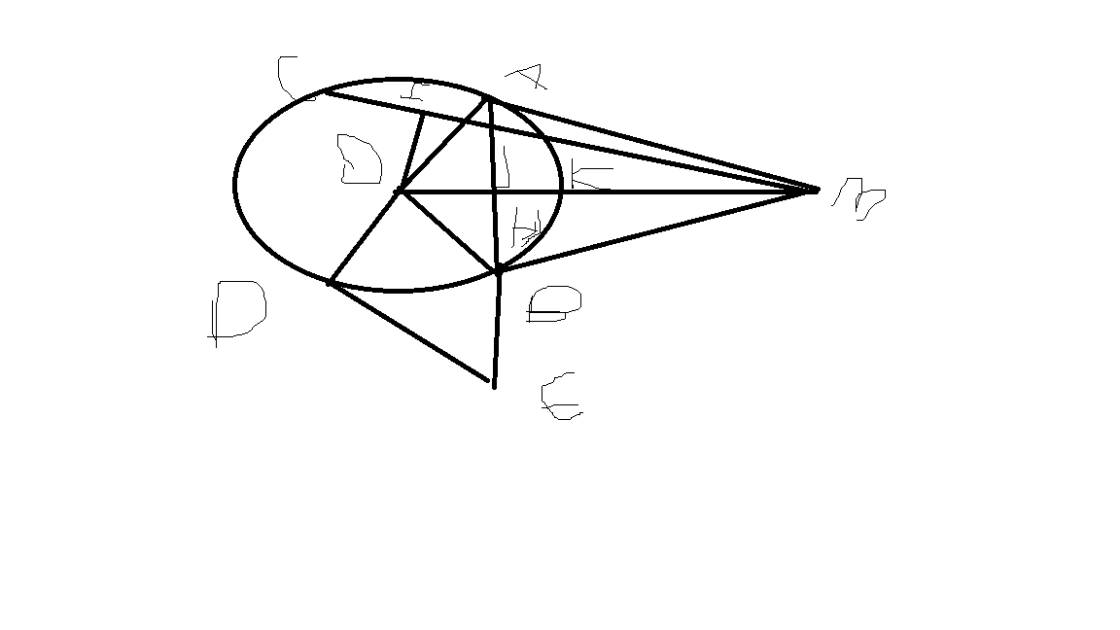
a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành

Vì \(\widehat{BEC}=\widehat{BKC}=90^0\)(góc nt chắn nửa đg tròn) nên \(HK\perp MC;ME\perp HC\)
Xét tam giác HMC có 2 đường cao HK,ME (cm trên) cắt nhau tại B nên B là trực tâm
Do đó BC⊥MH
