Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Chu kì T=0,5(s)
Thời điểm t=0 hoặc t=2s=4T thì vật ở cùng 1 vị trí và cùng 1 trạng thái
Tức là: tại t=0,vật có v>0 và \(a=-\omega^2x=80\pi^2\sqrt{2}\)
\(\Rightarrow x=-5\sqrt{2}=-\frac{A\sqrt{2}}{2}\)
+) Tại \(t=t_1=\frac{T}{8}\), vật ở li độ x=0, v>0
Tại \(t=t_2=\frac{T}{8}+\frac{T}{4}\), vật đi đến li độ x=A
Suy ra quãng đường vật đi được là: \(s=A\)
Tốc độ trung bình (đừng nhầm với vận tốc) của vật là:
\(\overline{v}=\frac{s}{\Delta t}=\frac{10}{0,1875-0,0625}=80\left(\frac{cm}{s}\right)\)
Chọn C

Chọn đáp án A
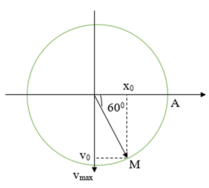
Chu kì dao động của vật:
T = 2 ( t 2 − t 1 ) = 1 , 5 s
v t b = 2 A Δ t ⇒ A = v t b Δ t 2 = 6 c m
Thời điểm t 1 = 1,75s ứng với góc
Δ φ = ω t 1 = 7 π 3 = 2 π + π 3 .
Giả sử thời điêm t 1 vật đang ở biên dương, sử dụng quay ngược lại trước đó 7 π / 3 rad ta xác định được thời điểm t 0 như hình vẽ. Từ đó ta suy ra:
x 0 v 0 = A 2 3 2 v max = 3 4 ω A 2 = 12 π 3

Vật dao động theo quỹ đạo thẳng dài 14 cm tức là \(2A = 14cm => A = 7cm.\)
Dựng đường tròn tương ứng với dao động của vật (Chiều dương ngược chiều kim đồng hồ)
7 -7 3,5 φ N M x 0 P
Điểm \(M\) và \(N\) đều có li độ là 3,5 cm nhưng chỉ có điểm \(M\) chuyển động theo chiều dương của trục x.
\(a_{min} = - \omega ^2 x_{min}\)=> vị trí vật có gia tốc cực tiểu là \(x_{min} = - 7 cm \) tương ứng với điểm \(P\) trên hình vẽ.
Vật sẽ đi từ \(M \rightarrow P \rightarrow P.\)
\(M \rightarrow P: t_1 = \frac{\varphi}{\omega} = \frac{\pi + \pi/3}{2\pi} = \frac{2}{3}s; S_1 = 3,5+ 2.7 = 17,5cm.\)
\(P \rightarrow P: t_2 = T= 1s; S_2 = 4.A= 4.7 = 28cm.\)
Vận tốc trung bình là \(v = \frac{quãng đường đi được}{thơi gian}\)
=> \(v = \frac{S_1+S_2}{t_1 + t_2} = \frac{17.5+28}{2/3+1} = 27,3cm/s.\)
Chọn đáp án.A.27,3cm.
câu này đáp án là 27 cm nhé
và vị trí gia tốc có giá trị cực tiểu là biên dương chứ không phải biên âm
![]()
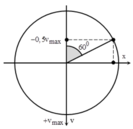


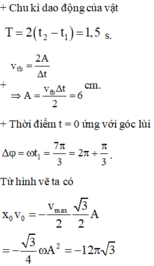
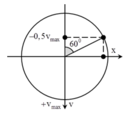
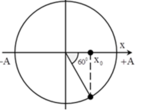


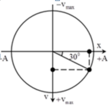

\(\omega=2\pi f=\pi; T=\frac{1}{f}=2\left(s\right)\)
\(t=2,5=T+\frac{T}{4}\)
\(A=\sqrt{x^2+\frac{v^2}{\omega^2}}=4\sqrt{2}\left(cm\right)\)
Suy ra, tại t1=0, vật đang ở li độ \(x=\frac{A\sqrt{2}}{2}\) theo chiều âm
Do đó, tại t=t2, vật đã đi được 1 quãng đường là: \(S=4A+A\sqrt{2}=8+16\sqrt{2}\left(cm\right)\)
Tốc độ trung bình là: \(\overline{v}=\frac{S}{t}=\frac{8+16\sqrt{2}}{2,5}\approx12,25\)
Chọn B