Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
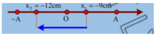

+ Tốc độ dao động trung bình của vật giữa hai thời điểm đó:
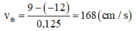

+ Chu kì dao động điều hòa: T = 1 / f = 0 , 5 ( s ) .
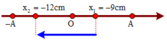
+ Vì thời gian 0 , 125 s = T / 4 nên vật đi từ x 1 = 9 c m đ ế n x 2 = - 12 c m theo chiều âm
(nếu đi theo chiều dưong đến x = A r ồ i q u a y l ạ i x 2 = - 12 c m thì cân thời gian lớn hơn T/4 )
+ Tốc độ dao động trang bình của vật giữa hai thời điểm đó: v t b = 9 − − 12 0 , 125 = 168 c m / s
Chọn đáp án B

Tại thời điểm t, vật đi qua vị trí có li độ x = -3 theo chiều dương.
Gia tốc có giá trị cực tiểu tại vị trí biên dương → gia tốc cực tiểu lần thứ 3 khi vật đi từ thời điểm t đến biên lần đầu tiên rồi tiếp tục chuyển động hai chu kì nữa.
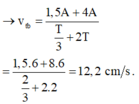
Đáp án A

Hướng dẫn bạn:
- Lực kéo về: \(F=k.x=0,03\sqrt 2\pi\) (không biết có đúng như giả thiết của bạn không)
\(\Rightarrow x =\dfrac{0,03\sqrt 2\pi}{k}=\dfrac{0,03\sqrt 2\pi}{m.\omega^2}=\dfrac{0,03\sqrt 2\pi}{0,01.\omega^2}=\dfrac{3\sqrt 2\pi}{\omega^2}\)
- Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 0,05^2=(\dfrac{3\sqrt 2\pi}{\omega^2})^2+\dfrac{(0,4\pi)^2}{\omega^2}\)
Bạn giải pt trên tìm \(\omega \) và suy ra chu kì \(T\) nhé.

\(\omega=2\pi f=\pi; T=\frac{1}{f}=2\left(s\right)\)
\(t=2,5=T+\frac{T}{4}\)
\(A=\sqrt{x^2+\frac{v^2}{\omega^2}}=4\sqrt{2}\left(cm\right)\)
Suy ra, tại t1=0, vật đang ở li độ \(x=\frac{A\sqrt{2}}{2}\) theo chiều âm
Do đó, tại t=t2, vật đã đi được 1 quãng đường là: \(S=4A+A\sqrt{2}=8+16\sqrt{2}\left(cm\right)\)
Tốc độ trung bình là: \(\overline{v}=\frac{S}{t}=\frac{8+16\sqrt{2}}{2,5}\approx12,25\)
Chọn B

Đáp án A
Hai thời điểm vuông pha nhau, ta có A = x 1 2 + x 2 2 = 5


+) Chu kì T=0,5(s)
Thời điểm t=0 hoặc t=2s=4T thì vật ở cùng 1 vị trí và cùng 1 trạng thái
Tức là: tại t=0,vật có v>0 và \(a=-\omega^2x=80\pi^2\sqrt{2}\)
\(\Rightarrow x=-5\sqrt{2}=-\frac{A\sqrt{2}}{2}\)
+) Tại \(t=t_1=\frac{T}{8}\), vật ở li độ x=0, v>0
Tại \(t=t_2=\frac{T}{8}+\frac{T}{4}\), vật đi đến li độ x=A
Suy ra quãng đường vật đi được là: \(s=A\)
Tốc độ trung bình (đừng nhầm với vận tốc) của vật là:
\(\overline{v}=\frac{s}{\Delta t}=\frac{10}{0,1875-0,0625}=80\left(\frac{cm}{s}\right)\)
Chọn C