Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kí hiệu \(N_{01}\), \(N_{02}\) là số hạt ban đầu lần lượt của \(^{235}U\) và \(^{238}U\).
t = 0 Ban đầu t thời điểm cần xác định hiện nay t 1 2
Hiện nay \(t_2\): \(\frac{N_{1}}{N_{2}}=\frac{N_{01}2^{-\frac{t_2}{T_1}}}{N_{02}2^{-\frac{t_2}{T_2}}} =\frac{7}{1000}.(1)\)
Thời điểm \(t_1\):
\(\frac{N_1}{N_2}= \frac{N_{01}2^{-\frac{t_1}{T_1}}}{N_{02}2^{-\frac{t_1}{T_2}}} = \frac{3}{100}.(2)\)
Chia (1) cho (2) => \(\frac{2^{-\frac{t_2}{T_1}}.2^{-\frac{t_1}{T_2}}}{2^{-\frac{t_1}{T_1}}.2^{-\frac{t_2}{T_2}}}= \frac{7.100}{3.1000}= \frac{7}{30}.\)
Áp dụng \(\frac{1}{2^{-x}} =2^x. \)
=> \(2^{(t_2-t_1)(\frac{1}{T_2}-\frac{1}{T_1})} = \frac{7}{30}.\)
=> \(t_2-t_1 = \frac{T_1T_2}{T_1-T_2}\ln_2 (7/30)=1,74.10^{9}\).(năm) \(= 1,74 \)(tỉ năm).
Như vậy cách hiện nay 1,74 tỉ năm thì trong urani tự nhiên có tỉ lệ số hạt thỏa mãn như bài cho.

Cứ 1 hạt nhân \(_{92}^{238}U\) bị phân rã tạo ra 1 hạt nhân \(_{82}^{206}Pb\). Từ đó ta có nhận xét là số hạt nhân \(_{92}^{238}U\) bị phân rã chính bằng số hạt nhân \(_{82}^{206}Pb\) tạo thành.
Tỉ số giữa số hạt nhân \(_{92}^{238}U\) bị phân rã và số hạt nhân \(_{92}^{238}U\) còn lại là
\(\frac{\Delta N}{N}= \frac{6,239.10^{18}}{1,188.10^{20}}= 0,0525 = \frac{1-2^{-\frac{t}{T}}}{2^{-\frac{t}{T}}}\)
Nhân chéo => \(2^{-\frac{t}{T}}= 0,95.\)
=> \(t = -T\ln_2 0,95 = 3,3.10^8\)(năm)
=> Tuổi của khối đã là 3,3.108 năm.

\(_{92}^{238}U \rightarrow _2^4He + _{90}^{234}\text{Th}\)
Sau 9.109 năm thì số gam Urani bị phân rã là
\(\Delta m = m_0 - m(t) = m_0(1-2^{-t/T}) = 6,97g.\)
Số mol urani bị phân rã là \(n = \frac{\Delta m}{A_{U}} = \frac{6,97}{238} = 0,0293 \text{mol}.\)
Dựa vào phương trình ta thấy cứ 1 hạt Urani bị phân rã sẽ tạo thành 1 hạt Thori. Suy ra \(n_{Th} = n_{urani}\)
Nhưu vậy khối lượng Thori tạo thành là \(m_{Th} = 0,0293.234 = 6,854 g.\)

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Đáp án D
Chất phóng xạ Urani U 92 235 phóng xạ α tạo thành Thôri (Th)
+Tại một thời điểm nào đó tỉ lệ giữa số nguyên tử Th và nguyên tử U 92 235 bằng 2:
N t h N U = 2
Sau thời gian t số nguyên tử U đã phân rã (cũng chính là số nguyên tử Th tạo ra)
N 1 = N o ( 1 - 2 - 1 T )
Ban đầu (t=0) không có Th, chỉ có U nên 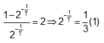
+Sau thời điểm đó ∆ t thì tỉ lệ số nguyên tử nói trên bằng 23
Số nguyên tử U đã phân rã (cũng chính là số nguyên tử Th tạo ra)
N 2 = N o ( 1 - 2 - t + ∆ t T )
Theo đó 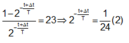
Từ (1) và (2) ta có ∆ t = 3 T = 21 , 9 . 10 8

1 hạt nhân \(_6^{14}C\) bị phân rã tạo thành 1 hạt nhân \(_7^{14}N\).
Tỉ số giữa số nguyên tử đã bị phóng xạ và số nguyên tử ban đầu là
\(\frac{\Delta N}{N_0}= 1-2^{-\frac{t}{T}}= 0,875.\)
=> \(2^{-\frac{t}{T}}= 0,125= 2^{-3}.\)
=> \(t = 3T = 16710\)(năm).

Cách 1: Trong 5 μs = T/4 nên điện tích dịch chuyển là Q0
Số \( Ne = \frac{Q_0}{e} \text{ với } Q_0 = \frac{I_0}{\omega }\)
Đáp án A
Cách 2: Áp dụng \(q = n.e = \int_{0}^{5.10^{-6}} 0,012.\sin (10^5 \pi t) dt = 3,82.10^{-8}C \Rightarrow n = \frac{q}{e } = \frac{3,82.10^{-8}}{1,6.10^{-19}} = 2,39.10^{11}\)
Đáp án A

\(E_n = -\frac{13,6}{n^2},(eV)\)(với n = 1, 2, 3,..)
Nguyên tử hiđrô hấp thụ một phôtôn có năng lượng 2,55 eV.
Việc đầu tiên là cần phải xác định xem nguyên tử nhảy từ mức nào lên mức nào mà có hiệu năng lượng giữa hai mức đúng bằng 2,55 eV.
\(E_1 = -13,6eV\), \(E_3 = -1,51 eV\)
\(E_2 = -3,4eV\),\(E_4 = -0,85eV\)
Nhận thấy \(E_4-E_2= -0,85 +3,4= 2,55 eV.\)
Như vậy nguyên tử đã hấp thụ năng lượng và nhảy từ mức n = 2 lên mức n = 4.
Tiếp theo, nguyên tử đang ở mức n = 4 rồi thì nó có thể phát ra bước sóng nhỏ nhất ứng với từ n = 4 về n = 1 tức là \(\lambda_{41}\) thỏa mãn
\(\lambda_{41}= \frac{hc}{E_4-E_1}= \frac{6,625.10^{-34}.3.10^8}{(-0,85+13,6).1,6.10^{-19}}=9,74.10^{-8}m. \)
Đáp án D
Tại thời điểm đề bài cho, gọi số nguyên tử Th là NTh và số nguyên tử Urani là NU
Theo đề bài 1 Urani phóng xạ tạo thành 1 Thori.
Sau thời gian t tính từ thời điểm tỉ lệ bằng 2 thì số nguyên tử Urani còn lại: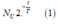
Và số nguyên tử Thori tạo ra sau thời gian t tính từ thời điểm tỉ lệ bằng 2 là:
Theo đề bài tỉ lệ giữa số nguyên tử sau thời gian t là 11 => (2) : (1) = 11
Thay (*) vào phương trình trên ta có:
Theo đề T = 7,13.108 (năm) => t = 2.7,13.108 = 14,26.108(năm)