Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

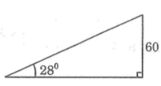
Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28 ° , chiều cao tòa nhà là cạnh đối với góc nhọn.
Vậy chiếc ô tô đang đỗ cách tòa nhà:
60.cotg 28 ° ≈ 112,844 (m)

Gọi vận tốc của người đi xe đạp là y km/ phút và vận tốc của xe khách là z km/ phút.
Xét trường hợp các xe khách đi cùng chiều với người đi xe đạp
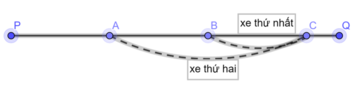
Giả sử xe khách thứ nhất vượt người đi xe đạp ở điểm B thì khi đó xe thứ hai đang ở điểm A. Như vậy, quãng đường AB là quãng đường mà xe khách phải đi trong x phút: AB = xz (km)
Gọi điểm mà xe thứ hai vượt người đi xe đạp là C thì quãng đường BC là quãng đường người đi xe đạp đi trong 15 phút: BC = 15y (km).
Quãng đường AC là quãng đường xe khách đi trong 15 phút nên AC = 15z (km).
Ta có phương trình: 15z = xz + 15y (1)
Xét trường hợp các xe khách đi ngược chiều với xe đạp

Giả sử người đi xe đạp gặp xe khách thứ nhất đi ngược chiều tại D thì xe thứ hai đi ngược chiều đang ở E. Hai xe khởi hành cách nhau x phút nên quãng đường
DE = xz (km)
Sau đó 10 phút người đi xe đạp gặp xe đi ngược chiều thứ hai nên đoạn DF là quãng đường xe đạp đi trong 10 phút: DF = 10y, đoạn FE là quãng đường xe khách đi được trong 10 phút: FE = 10z. Ta có phương trình: 10y + 10z = xz (2)
Từ (1) và (2) ta có hệ phương trình:
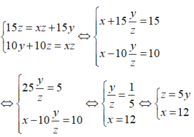
Vậy cứ 12 phút lại có một xe khách xuất phát và vận tốc xe khách gấp 5 lần vận tốc người đi xe đạp.

Đặt tam giác ABC vuông tại A với B là đỉnh tháp
Áp dụng tslg trong tam giác ABC vuông tại A:
\(tanC=\dfrac{AB}{AC}\)
\(\Rightarrow tan30^0=\dfrac{26}{AC}\)
\(\Rightarrow AC=\dfrac{26}{tan30^0}=26\sqrt{3}\left(m\right)\)