Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác PAOB có
góc PAO+góc PBO=180 độ
nên PAOB là tứ giác nội tiếp
b: Xét ΔQPD và ΔQAP có
góc QDP=góc QPA(=1/2*sđ cung AC)
góc PQD chung
=>ΔQPD đồng dạng với ΔQAP
=>QP/QA=QD/QP
=>QP^2=QA*QD

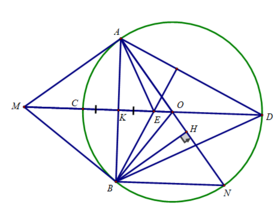
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB

a: Xét (O) có
AB là tiếp tuyến có B là tiếp điểm
AC là tiếp tuyến có C là tiếp điểm
Do đó: AB=AC
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của CB

Gọi E là giao của AO và MN
MN là đường trung bình của ΔABC
=>MN//BC
=>MN vuông góc AO tại E
PA^2=PE^2+AE^2
=AN^2-EN^2+OP^2-EO^2
=NC^2-EN^2+PQ^2+QO^2-EO^2
=NO^2-R^2+PQ^2+R^2-NO^2
=PQ^2
=>PA=PQ
Xét ΔQDP và ΔQPA có
góc QDP=góc QPA
góc DQP chung
=>ΔQDP đồng dạng với ΔQPA
=>QD/QP=QP/QA
=>QP^2=QD*QA