Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

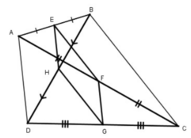
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình vuông khi và chỉ khi EFGH là hình chữ nhật đồng thời là hình thoi
⇔ AD ⊥ BC và AD = BC
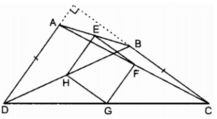

Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình thoi ⇔ EH = EF ⇔ AD = BC

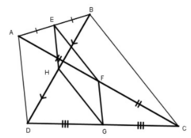
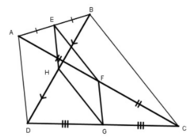
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AD ⊥ BC
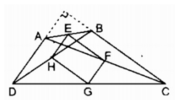

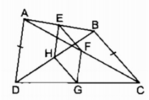
a: Xét ΔBAD có
E là tđiểm của AB
H là tđiểm của BD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//AD và EH=AD/2(1)
Xét ΔACD có
F là trung điểm của AC
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔACD
Suy ra: FG//AD và FG=AD/2(2)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EFGH là hình bình hành
Xét ΔABC có
E,H lần lượt là trung điểm của AB,AC
=>EH là đường trung bình của ΔABC
=>EH//BC và EH=BC/2
Xét ΔBDC có
F,G lần lượt là trung điểm của DB,DC
=>FG là đường trung bình của ΔBDC
=>FG//BC và FG=BC/2
EH//BC
FG//BC
Do đó: EH//FG
EH=BC/2
FG=BC/2
Do đó: EH=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
Xét ΔBAD có
E,F lần lượt là trung điểm của BA,BD
=>EF là đường trung bình
=>EF//AD và EF=AD/2
Để EHGF là hình vuông thì EH=EF và EH\(\perp\)EF
EH=EF
EH=BC/2
EF=AD/2
Do đó: BC=AD
EH\(\perp\)EF
EH//BC
Do đó: EF\(\perp\)BC
EF\(\perp\)BC
EF//AD
Do đó: BC\(\perp\)AD
Vậy: Khi BC=AD và BC\(\perp\)AD thì EFGH là hình vuông