HN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 8 2021
a: Xét tứ giác ABCD có
\(\widehat{B}+\widehat{D}=180^0\)
nên ABCD là tứ giác nội tiếp
30 tháng 11 2021
a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
16 tháng 4 2021
b) Xét ΔFDC có
A\(\in\)FD(gt)
B\(\in\)FC(gt)
AB//CD(gt)
Do đó: \(\dfrac{FA}{AD}=\dfrac{FB}{BC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{FA}{FB}=\dfrac{AD}{BC}=1\)
hay FA=FB
Ta có: FA+AD=FD(A nằm giữa F và D)
FB+BC=FC(B nằm giữa F và C)
mà FA=FB(cmt)
và AD=BC(ABCD là hình thang cân)
nên FD=FC
Ta có: FA=FB(cmt)
FD=FC(cmt)
Do đó: \(FA\cdot FD=FB\cdot FC\)(đpcm)
16 tháng 4 2021
a) Ta có: ABCD là tứ giác nội tiếp(gt)
nên \(\widehat{A}+\widehat{C}=180^0\)(hai góc đối)(1)
Ta có: ABCD là hình thang(AB//CD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)(2)
Từ (1) và (2) suy ra \(\widehat{C}=\widehat{D}\)
Hình thang ABCD(AB//CD) có \(\widehat{C}=\widehat{D}\)(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)
DH
0
CM
13 tháng 4 2017
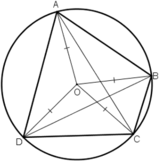
Tứ giác ABCD có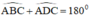 
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB .
Vậy các đường trung trực của AC, BD, AB cùng đi qua O.
HH
18 tháng 1 2021
- Tứ giác ABCD có \(\widehat{ABC}+\widehat{ADC}=180^o\)mà hai góc ABC và ADC là 2 góc ở vị trí đối nhau
=> Tứ giác ABCD là tứ giác nội tiếp
- Gọi O là tâm của đường tròn ngoại tiếp tứ giác ABCD , khi đó OA = OB = OC = OD ( cùng bán kính của đường tròn ( O ))
+) Vì OA = OB nên O thuộc đường trung trực của đoạn thằng AB
+) Vì OA = OC nên O thuộc đường trung trực của đoạn thẳng AC
+) VÌ OD = OB nên O thuộc đường trung trực của đoạn thằng BD
Do đó các đường trung trực của AB , BD cùng đi qua tâm O của đường tròn ngoại tiếp tứ giác ABCD
CM
12 tháng 2 2018
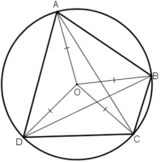
Tứ giác ABCD có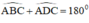 
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB .
Vậy các đường trung trực của AC, BD, AB cùng đi qua O.
Kiến thức áp dụng
+ Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 180º thì tứ giác đó nội tiếp một đường tròn.
CM
19 tháng 1 2018
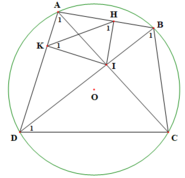
a) Tứ giác AHIK có:
A H I ^ = 90 0 ( I H ⊥ A B ) A K I ^ = 90 0 ( I K ⊥ A D ) ⇒ A H I ^ + A K I ^ = 180 0
=> Tứ giác AHIK nội tiếp.
b) ∆ IAD và ∆ IBC có:
A ^ 1 = B ^ 1 (2 góc nội tiếp cùng chắn cung DC của (O))
A I D ^ = B I C ^ (2 góc đối đỉnh)
=> ∆ IAD ~ ∆ IBC (g.g)
⇒ I A I B = I D I C ⇒ I A . I C = I B . I D
c, Xét đường tròn ngoại tiếp tứ giác AHIK có K ^ 1 = D ^ 1
A ^ 1 = H ^ 1 (2 góc nội tiếp cùng chắn cung IK)
mà A ^ 1 = B ^ 1 ⇒ H ^ 1 = B ^ 1
Chứng minh tương tự, ta được K ^ 1 = D ^ 1
∆ HIK và ∆ BCD có: H ^ 1 = B ^ 1 ; K ^ 1 = D ^ 1
=> ∆ HIK ~ ∆ BCD (g.g)
d) Gọi S1 là diện tích của ∆ BCD.
Vì ∆ HIK ~ ∆ BCD nên:
S ' S 1 = H K 2 B D 2 = H K 2 ( I B + I D ) 2 ≤ H K 2 4 I B . I D = H K 2 4 I A . I C (1)
Vẽ A E ⊥ B D , C F ⊥ B D ⇒ A E / / C F ⇒ C F A E = I C I A
∆ ABD và ∆ BCD có chung cạnh đáy BD nên:
S 1 S = C F A E ⇒ S 1 S = I C I A (2)
Từ (1) và (2) suy ra
S ' S 1 ⋅ S 1 S ≤ H K 2 4 I A . I C ⋅ I C I A ⇔ S ' S ≤ H K 2 4 I A 2 (đpcm)