Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{A}+\widehat{B}=360^0-70^0-80^0=210^0\)
mà \(\widehat{A}-\widehat{B}=20^0\)
nên \(\widehat{A}=\dfrac{210^0+20^0}{2}=115^0\)
=>\(\widehat{B}=115^0-20^0=95^0\)

1:
Xét ΔCHD có \(\widehat{CHD}+\widehat{HCD}+\widehat{HDC}=180^0\)
=>\(\widehat{HCD}+\widehat{HDC}=180^0-110^0=70^0\)
=>\(\dfrac{1}{2}\left(\widehat{ADC}+\widehat{BCD}\right)=70^0\)
=>\(\widehat{ADC}+\widehat{BCD}=140^0\)
Xét tứ giác ABCD có
\(\widehat{ADC}+\widehat{BCD}+\widehat{DAB}+\widehat{ABC}=360^0\)
=>\(\widehat{DAB}+\widehat{ABC}=220^0\)
mà \(\widehat{DAB}-\widehat{ABC}=40^0\)
nên \(\widehat{ABC}=\dfrac{220^0-40^0}{2}=90^0\)
=>BA\(\perp\)BC
2:
Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-220^0=140^0\)
=>\(2\cdot\left(\widehat{KCD}+\widehat{KDC}\right)=140^0\)
=>\(\widehat{KCD}+\widehat{KDC}=70^0\)
Xét ΔCKD có
\(\widehat{CKD}+\widehat{KCD}+\widehat{KDC}=180^0\)
=>\(\widehat{CKD}=180^0-70^0=110^0\)

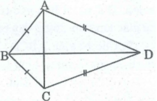
Xét ∆ BAD và ∆ BCD, ta có:
BA = BC (gt)
DA = DC (gt)
BD cạnh chung
Suy ra: ∆ BAD = ∆ BCD (c.c.c)
⇒ ∠ (BAD) = ∠ (BCD)
Mặt khác, ta có: ∠ (BAD) + ∠ (BCD) + ∠ (ABC) + ∠ (ADC) = 360 0
Suy ra: ∠ (BAD) + ∠ (BCD) = 360 0 – ( ∠ (ABC) + ∠ (ADC) )
2 ∠ (BAD) = 360 0 - 100 0 + 70 0 = 190 .
⇒ ∠ (BAD) = 190 0 : 2 = 95 0
⇒ ∠ (BCD) = ∠ (BAD) = 95 0

Chọn A. ∠ (C ) = 110 0
Ta có : ∠ (A )+ ∠ (D )= 180 0 ( hai góc trong cùng phía)
=> ∠ (D )= 180 0 - ∠ (A )= 180 0 - 70 0 = 110 0
mà ∠ (C )= ∠ (D ) (tính chất hình thang cân ) => ∠ (C )= ∠ (D )= 110 0

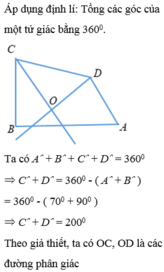

C