Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

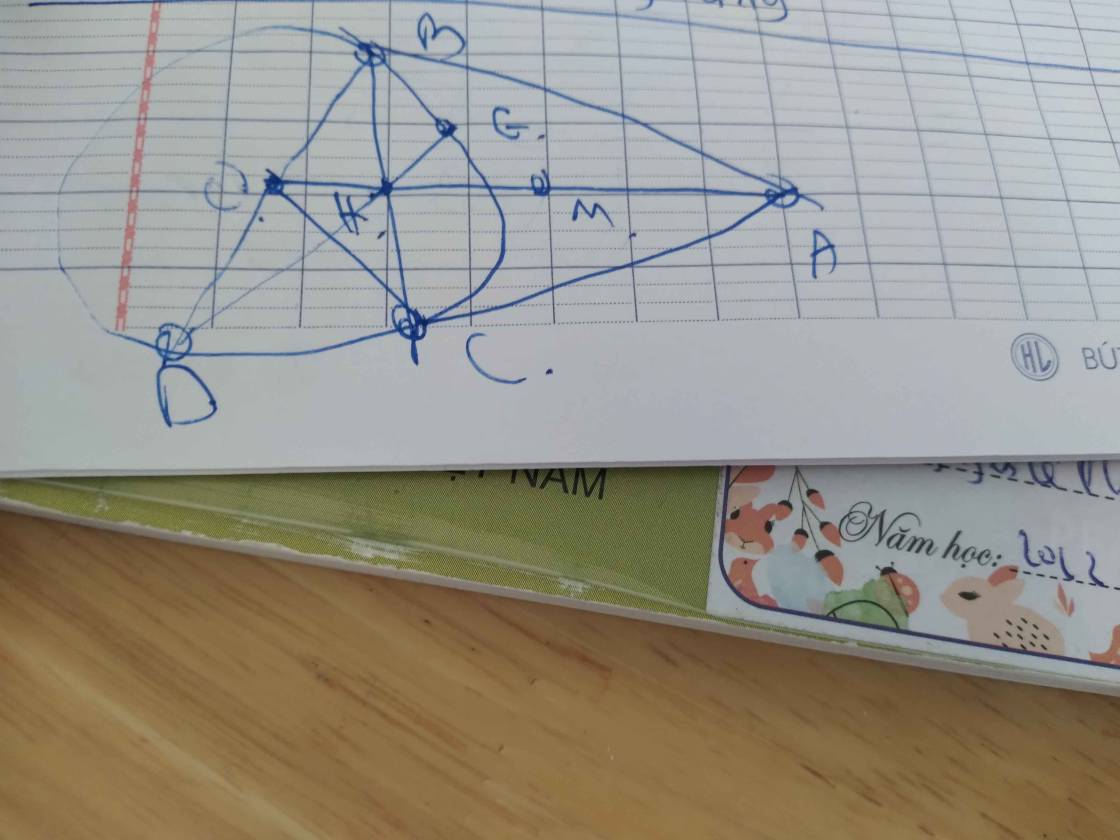
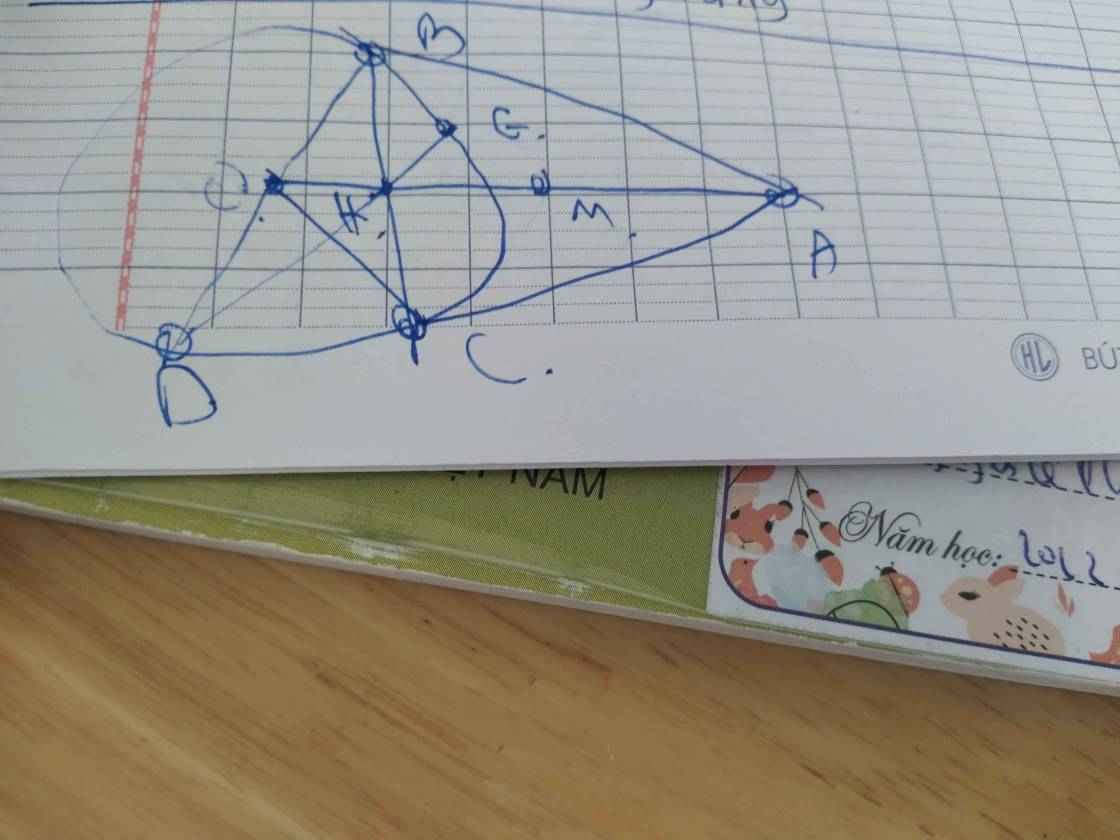
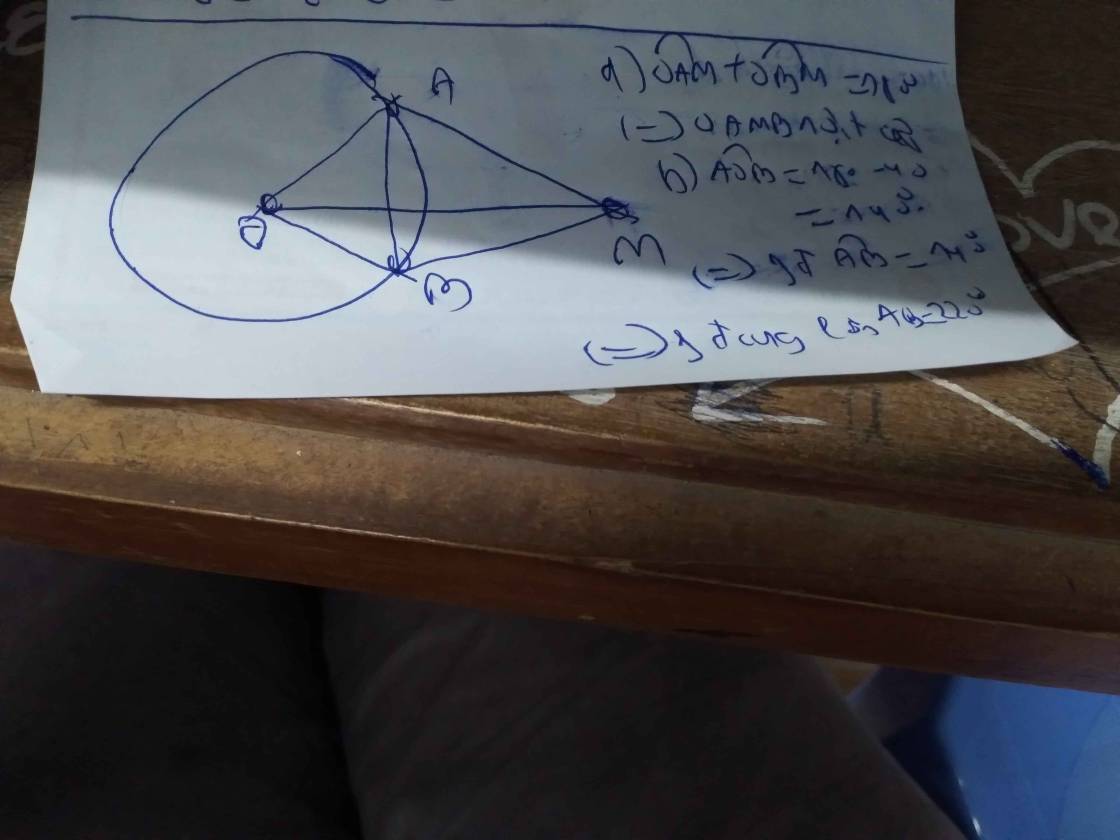
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp đường tròn đường kính MO
Tâm là trung điểm của MO
Bán kính là MO/2
b: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB
góc ABK=1/2*sđ cung AK=90 độ
=>AB vuông góc BK
=>BK//OM

Mình không vẽ được hình mong bạn thông cảm
a, Chắc bạn làm rồi
b, Sử dụng tính chất 2 tiếp tuyến cắt nhau
=>\(\hept{\begin{cases}AP=IP\\IQ=BQ\\MA=MB\end{cases}}\)
Khi đó \(P_{MPQ}=MP+AP+MQ+QB=MA+MB=2a\)(đpcm)
c, Vì H là trực tâm của tam giác MAB
=>\(AH\perp MB\)
MÀ \(MB\perp OB\)
=> \(AH//OB\)
CMTT=>\(BH//AO\)
=> tứ giác AHBO là hình bình hành
=>AH=OB=R
MÀ A cố định
=> \(H\in\left(A,R\right)\)cố định
Vậy H thuộc đường tròn tâm A bán kính R cố định

a, Chứng minh được DBOF nội tiếp đường tròn tâm I là trung điểm của DO
b, O A = O F 2 + A F 2 = 5 R 3 => cos D A B ^ = A F A O = 4 5
c, ∆AMO:∆ADB(g.g) => D M A M = O B O A
mà M O D ^ = O D B ^ = O D M ^ => DM = OM
=> D B D M = D B O M = A D A M . Xét vế trái B D D M - D M A M = A D - D M A M = 1
d, D B = A B . tan D A B ^ = 8 R 3 . 3 4 = 2 R => O M = A O . tan D A B ^ = 5 R 4
=> S O M D B = 13 R 2 8
S O M D B ngoài = S O M D B - 1 4 S O , R = R 2 8 13 - 2 π