Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì AE là phân giác \(\widehat{BAC}\)
\(\Rightarrow\) \(\widehat{BAE}=\widehat{EAC}\) hay \(\widehat{BAD}=\widehat{EAC}\)
Xét (O) có: \(\widehat{CBA}=\widehat{AEC}\)(cùng chắn \(\stackrel\frown{AC}\))
hay \(\widehat{DBA}=\widehat{AEC}\)
Xét ΔBAD và ΔEAC có:
\(\widehat{BAD}=\widehat{EAC}\) (cmtrn)
\(\widehat{DBA}=\widehat{AEC}\) (cmtrn)
\(\Rightarrow\) ΔBAD∼ΔEAC (g.g)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AC}\) \(\Leftrightarrow AB.AC=AE.AD\) (đpcm)
b) Theo CM a) ΔBAD∼ΔEAC
\(\widehat{BDA}=\widehat{ECA}\) hay \(\widehat{SDA}=\widehat{ECA}\) (1)
Xét (O) có: \(\widehat{ECA}=\widehat{EAS}\) (cùng chắn \(\stackrel\frown{EA}\))
hay \(\widehat{ECA}=\widehat{DAS}\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\widehat{SDA}=\widehat{DAS} \) \((=\widehat{ECA})\)
\(\Rightarrow\) ΔDSA cân tại S
c) Xét (O) có: \(\widehat{BCA}=\widehat{BAS}\) (cùng chắn \(\stackrel\frown{AB}\))
hay \(\widehat{SCA}=\widehat{BAS}\)
Xét ΔCSA và ΔASB có:
\(\widehat{CSA}:chung\)
\(\widehat{SCA}=\widehat{BAS}\)
\(\Rightarrow\) ΔCSA∼ΔASB (g.g)
\(\Rightarrow\frac{SC}{SA}=\frac{SA}{SB}\) \(\Leftrightarrow SC.SB=SA^2\) (đpcm)
d) Xét (O) có: \(\widehat{ECP}=\widehat{EAC}\) (cùng chắn \(\stackrel\frown{EC}\))
hay \(\widehat{QCP}=\widehat{EAC}\) (3)
Theo CM a) \(\widehat{BAE}=\widehat{EAC}\) hay \(\widehat{QAP}=\widehat{EAC}\) (4)
Từ (3) và (4) \(\Rightarrow\) \(\widehat{QCP}=\widehat{QAP}\) \((=\widehat{EAC})\)
\(\Rightarrow\) Tứ giác QACP nội tiếp đường tròn (theo dhnb tứ giác nội tiếp).

a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
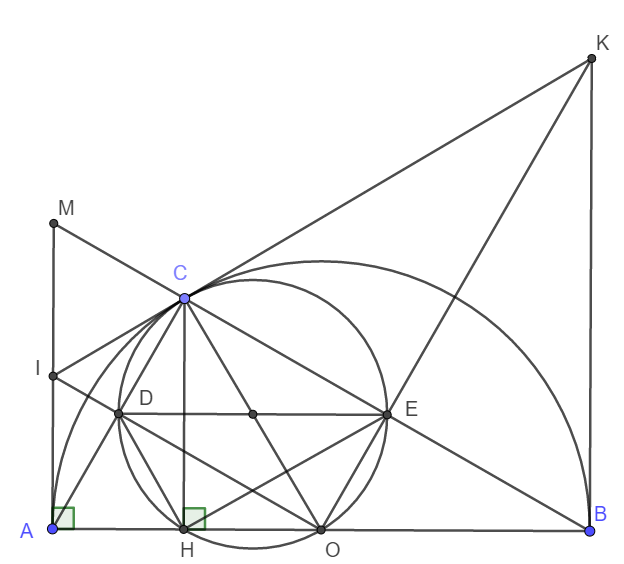
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.

Tự vẽ hình nha
c) AE là tia phân giác của góc CAB => sđcEC=sđcEB=> EC=EB=> OE vuông góc vs BC
Góc OAE= góc OEA(1)
OE song song vs AH (cùng vuông góc vs BC)=> OEA=EAH(2)
Từ (1) và (2) => góc OAE= góc EAH => AE là tia phân giác của góc OAH
Câu f)
Theo phần d đã chứng minh được $BHOC$ nội tiếp
\(\Rightarrow \widehat{MHB}=\widehat{MCO}\)
Xét tam giác $MHB$ và $MCO$ có:
\(\left\{\begin{matrix} \widehat{MHB}=\widehat{MCO}\\ \text{Chung góc M}\end{matrix}\right.\Rightarrow \triangle MHB\sim \triangle MCO(g.g)\)
\(\Rightarrow \frac{MB}{HB}=\frac{MO}{CO}(1)\)
Giờ ta sẽ chứng minh \(\frac{MO}{CO}=\frac{KM}{KH}\)
\(\Leftrightarrow MO.KH=KM.CO\)
\(\Leftrightarrow MO.KH=CO(MO+OK)\)
\(\Leftrightarrow CO.OK=MO(KH-CO)=MO(KH-KO)\)
\(\Leftrightarrow CO^2=MO.OH\)
\(\Leftrightarrow OA^2=OH.OM\) (đúng theo hệ thức lượng trong tam giác vuông MAO)
Do đó \(\frac{MO}{CO}=\frac{KM}{KH}\). Kết hợp với (1) suy ra \(\frac{KM}{KH}=\frac{BM}{BH}\Rightarrow MK.BH=BM.HK\)
Bạn ơi, mình học là cái dấu hiệu góc ngoài tại 1 đỉnh bằng góc trong tại định đó chỉ được dùng để chứng minh chứ không được dùng làm định lí
Giờ sao ???