Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

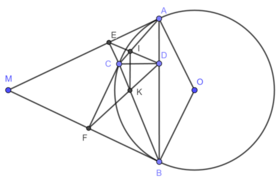
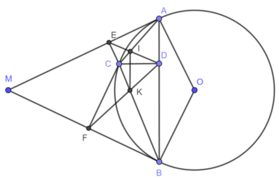
a. Vì \(CE\perp MA\)tại E (gt) => \(\widehat{AEC}=90^o\)
\(CD\perp AB\)tại D=> \(\widehat{ADC}=90^o\)
Xét tứ giác AECD có: \(\widehat{AEC}+\widehat{ADC}=90^o+90^o=180^o\)=> AECD là tứ giác nội tiếp đt \((G,R=\frac{AC}{2})\)trong đó G là trung điểm của AC (dhnb)
Cmtt ta có: BFCD là tứ giác nội tiếp đt \((H,R=\frac{BC}{2})\)trong đó H là trung điểm của BC
b.
Vì AECD là tứ giác nội tiếp (cmt) => \(\widehat{EAC}=\widehat{EDC}\)(2 góc nội tiếp cùng chắn \(\widebat{EC}\)) (1)
Do MA là tiếp tuyến của đt(O) (gt)=> \(\widehat{EAC}=\frac{1}{2}sđ\widebat{AC}\)(t/c góc tạo bởi tiếp tuyến và dây cung)
Xét đt (O) có: \(\widehat{ABC}=\widehat{DBC}=\frac{1}{2}sđ\widebat{AC}\)(t/c góc nội tiếp) => \(\widehat{EAC}=\widehat{DBC}\)(2)
vì BFCD là tứ giác nội tiếp => \(\widehat{DBC}=\widehat{DFC}\)(2 góc nội tiếp cùng chắn \(\widebat{DC}\)) (3)
Từ (1),(2) và (3) => \(\widehat{EDC}=\widehat{DFC}\)
do AECD là tứ giác nội tiếp (cmt) => \(\widehat{CED}=\widehat{CAD}\)(2 góc nội tiếp cùng chắn \(\widebat{CD}\)) (4)
Vì MB là tiếp tuyến của đt (O) tại B (gt) => \(\widehat{CBF}=\frac{1}{2}sđ\widebat{BC}\)(T/c góc tạo bởi tiếp tuyến và dây cung)
Xét đt (O) có: \(\widehat{BAC}=\widehat{DAC}=\frac{1}{2}sđ\widebat{BC}\)(t/c góc nội tiếp) => \(\widehat{CBF}=\widehat{DAC}\)(5)
lại có: BFCD là tứ giác nội tiếp (cmt) => \(\widehat{CBF}=\widehat{CDF}\)(2 góc nội tiếp cùng chắn \(\widebat{CF}\)) (6)
Từ (4), (5) và (6) => \(\widehat{CED}=\widehat{CDF}\)
Xét \(\Delta ECD\)và \(\Delta DCF\)có:
\(\widehat{CED}=\widehat{CDF}\)(Cmt)
\(\widehat{EDC}=\widehat{DFC}\)(Cmt)
=> \(\Delta ECD~\Delta DCF\)(g.g) => \(\frac{EC}{DC}=\frac{CD}{CF}\Rightarrow CD^2=CE\times CF\)(Đpcm)
c. Vì I là giao điểm của AC và DE (gt) => \(I\in AC\)
K là giao điểm của BC và DF (gt) => \(K\in BC\)
=> \(\widehat{ICK}=\widehat{ACB}\)
Vì \(\widehat{EDC}=\widehat{ABC}\left(cmt\right)\Rightarrow\widehat{IDC}=\widehat{ABC}\left(do\overline{E,I,D}\Rightarrow\widehat{EDC}=\widehat{IDC}\right)\)
\(\widehat{CDF}=\widehat{BAC}\left(cmt\right)\Rightarrow\widehat{CDK}=\widehat{BAC}\left(do\overline{F,K,D}\Rightarrow\widehat{CDF}=\widehat{CDK}\right)\)
Xét tứ giác ICKD có : \(\widehat{ICK}+\widehat{IDK}=\widehat{ICK}+\widehat{IDC}+\widehat{CDK}=\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\)
(Áp dụng định lý tổng 3 góc trong \(\Delta ABC\)ta có: \(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\))
=> Tứ giác ICKD là tứ giác nội tiếp (dhnb) => 4 điểm I,C,K,D cùng thuộc 1 đường tròn (đpcm)
d. Vì ICKD là tứ giác nội tiếp (cmt) => \(\widehat{CIK}=\widehat{CDK}\)(2 góc nội tiếp cùng chắn \(\widebat{CK}\))
Lại có: \(\widehat{CDK}=\widehat{BAC}\)(Cmt) => \(\widehat{CIK}=\widehat{BAC}\)mà 2 góc này ở vị tri đồng vị => IK // AB (Dhnb)
Do \(CD\perp AB\left(gt\right)\)=> \(IK\perp CD\)(Quan hệ tính vuông góc và tính song song của 3 đt)

Câu a, Tứ giác AECD có : CEA^=90* ; CDA^=90*
=>CEA^+CDA^=180*
=>AECD nội tiếp
Câu b, Xét tam giác BCD và tam giác ACE , có :
BDC^=CEA^=90*
CBA^=CAE^ ( góc nội tiếp ; góc ở tâm cùng chắn một cung )
=>Tam giác BCD ~ Tam giác ACE
=> BC/AC=CD/CE=BD/AE (1)
Xét tam giác CFB và tam giác CDA , có :
CFB^=CDA^=90*
CBF^=CAD^ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung )
=>Tam giác CFB ~ tam giác CDA ( g - g )
=>CF/CD=CB/CA=BF/AD (2)
Từ (1) và (2)
=>CD/CE=CF/CD
=>CD^2=CE.CF
Chúc bạn học tốt !

Lời giải:

a)
\(CD\perp AB, CE\perp AM, CF\perp MB\Rightarrow \left\{\begin{matrix} \widehat{CDA}=\widehat{CEA}=90^0\\ \widehat{CFB}=\widehat{CDB}=90^0\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} \widehat{CDA}+\widehat{CEA}=180^0\\ \widehat{CFB}+\widehat{CDB}=180^0\end{matrix}\right.\)
Tứ giác $AECD$ và $BFCD$ có tổng hai góc đối bằng $180^0$ nên là tứ giác nội tiếp.
b)
Từ kết quả 2 tứ giác nội tiếp trên, kết hợp với tính chất góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn dây cung đó ta có:
\(\widehat{CDF}=\widehat{CBF}=\widehat{CAB}=\widehat{CAD}=\widehat{CED}\)
\(\widehat{CFD}=\widehat{CBD}=\widehat{CBA}=\widehat{EAC}=\widehat{CDE}\)
Do đó \(\triangle CDF\sim \triangle CED(g.g)\)
\(\Rightarrow \frac{CD}{CF}=\frac{CE}{CD}\Rightarrow CD^2=CE.CF\)
c)
Theo phần b:
\(\widehat{IDK}=\widehat{CDF}+\widehat{CDE}=\widehat{EAC}+\widehat{FBC}\)
\(=\widehat{CBA}+\widehat{CAB}=180^0-\widehat{ACB}=180^0-\widehat{ICK}\)
\(\Rightarrow \widehat{IDK}+\widehat{ICK}=180^0\)
Do đó tứ giác $ICKD$ nội tiếp.