Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi a, b, c là 3 số. \(\begin{cases}\frac{a+b+c}{3}=20\\\frac{2a+b+c}{3}=24\\\frac{a+3b+c}{3}=32\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a+b+c=60\\2a+b+c=72\\a+3b+c=96\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a=12\\b=18\\c=30\end{cases}\)
Vậy, số thứ ba là 30.
Gọi x là số thứ nhất
y là số thứ hai
z là số thứ ba
Theo đề ta có hệ phương trình: \(\begin{cases}x+y+z=60\\2x+y+z=72\\x+3y+z=96\end{cases}\)
Giải hệ phương trình ta được: \(\begin{cases}x=12\\y=18\\z=30\end{cases}\)
Vậy số thứ ba là 30

gọi 4 số cần tìm lần lượt là a,b,c,d
theo đề ta có;
\(\frac{\left(a+b+c+d\right)}{4}=45\) (1)
a-2=b:2=c+2=2d
ta đặt: a-2=b:2=c+2=2d=k
suy ra a=k+2;b=2k;c=k-2;d=k:2 (2)
thay (2) vào (1), ta được:
\(\frac{\left(a+b+c+d\right)}{4}=45\)
\(\frac{\left(k+2+2k+k-2+\frac{k}{2}\right)}{4}=45\)
\(\frac{9}{2}k=180\)
\(k=40\)
\(\Rightarrow a=k+2=40+2=42\)
\(\Rightarrow b=2k=2.40=80\)
\(\Rightarrow c=k-2=40-2=38\)
\(\Rightarrow d=\frac{k}{2}=\frac{40}{2}=20\)

Gọi 4 số cần tìm lần lượt là \(a,b,c,d\) Theo bài ra ta có :\(\begin{cases}a=3c\\b=2c\\d=b+7\\a+b+c+d=143\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a-3c=0\\b-2c=0\\b-d=-7\\a+b+c+d=143\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a=51\\b=34\\c=17\\d=41\end{cases}\) (bấm máy hpt 4 ẩn)
Vậy 4 số cần tìm lần lượt là \(51;34;17;41\)

Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
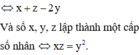
Cách giải:
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
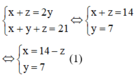
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân nên ta có:
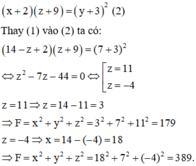


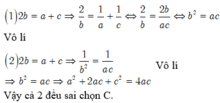
Tổng của ba số là \(75\cdot3=225\)
Viết thêm chữ số 0 vào bên phải số thứ hai thì được số thứ nhất nên số thứ nhất gấp 10 lần số thứ hai
Tỉ số giữa số thứ nhất và số thứ ba là \(10\cdot\dfrac{1}{4}=2,5\)
Số thứ ba là: \(\dfrac{225}{1+2,5+4}=30\)
Số thứ hai là 30:4=7,5
Số thứ nhất là \(30\cdot2,5=75\)