Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm có 8 vân sáng màu lục tức là khoảng cách đó là \(\Delta x _{min}= 9i_{lục}.\)
=> \(9i_{lục}= k_2 i_{đỏ}=> 9\lambda_{lục}= k_2 \lambda_{đỏ}\)
=> \(\lambda_{lục} = \frac{k_2 \lambda_{đỏ}}{9}.\ \ (1)\)
Mà \(500 n m \leq \lambda_{lục} \leq 575nm.\)
Thay (1) vào <=> \(500 n m \leq \frac{k_2 \lambda_{đỏ}}{9} \leq 575nm.\)
<=> \(\frac{500.9}{720} \leq k_2 \leq \frac{575.9}{720}\)
<=> \(6,25 \leq k_2 \leq 7,1875\)
=> \(k_2 = 7=> (1): \lambda_{lục} = 560nm.\)
720nm = 0,72 μm
giữa 2 vân sáng gần nhau nhất và cùng màu vs vân sáng trung tâm có 8 vân sáng màu lục => Tại vị trí trùng đó là VS bậc 9 của λlục
Tại VT trùng nhau: x_kđỏ = x_9lục
<=> kđỏ.λđỏ = 9.λlục
<=> kđỏ/9 = λlục/λđỏ = λ/0,72
=> λ = (0,72.kđỏ)/9 = 0,08.kđỏ (*)
0,5 ≤ λ = 0,08.kđỏ ≤ 0,575 μm
6,25 ≤ kđỏ ≤ 7,1875
=> kđỏ = 7
thế vào (*) λ = 0,56 (μm) = 560nm
đáp án : D

Đáp án C
+ Trên màn, trong khoảng giữa hai vân sáng gần nhau nhất và cùng màu với vân sáng trung tâm có 8 vân sáng lục nên vân sáng lục trùng nhau là vân thứ 9: k1=9
+ Điều kiện trùng nhau của hai bức xạ:
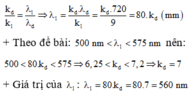

Khoảng cách giữa hai vân sáng cùng màu gần nhất với vân chính giữa là : x = k1 i1 = k2 i2 => k1λ1 = k2λ2
Nhận xét: k2 = 9 => k1.720 = 9 λ2 => λ2 = 80 k1.
Do λ2 có giá trị trong khoảng từ 500nm đến 575nm nên dễ thấy k1 = 7
=> λ2 = 560 nm.
Đáp án D

Ta có: \(i_1=3,5/7=0,5mm\)
\(i_2=7,2/8=0,9mm\)
Vân sáng: \(i=\dfrac{\lambda D}{a}\)
Suy ra: \(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}\Rightarrow \lambda_2=\lambda_1.\dfrac{i_2}{i_1}=420.\dfrac{0,9}{0,5}=756nm\)

Khi các vân sáng trùng nhau: \(k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)
k10,4 = k20,5 = k30,6 \(\Leftrightarrow\) 4k1 = 5k2 = 6k3
BSCNN(4,5,6) = 60
\(\Rightarrow\) k1 = 15 ; k2 = 12 ; k3 = 10 Bậc 15 của \(\lambda_1\) trùng bậc 12 của \(\lambda_2\) trùng với bậc 10 của \(\lambda_3\)
Trong khoảng giữa phải có: Tổng số VS tính toán = 14 + 11 + 9 = 34
Ta xẽ lập tỉ số cho tới khi k1 = 15 ; k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_2:\) \(\frac{k_1}{k_2}=\frac{\lambda_1}{\lambda_2}=\frac{5}{4}=\frac{10}{8}=\frac{15}{12}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k2 = 12 thì có tất cả 4 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 5 ; k2 = 4
Vị trí 3: k1 = 10 ; k2 = 8 => Trong khoảng giữa có 2 vị trí trùng nhau.
Vị trí 4: k1 = 15 ; k2 = 12
- Với cặp\(\lambda_2;\lambda_3:\) \(\frac{k_2}{k_3}=\frac{\lambda_3}{\lambda_2}=\frac{6}{5}=\frac{12}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k2 = 12 ; k3 = 10 thì có tất cả 3 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k2 = 6 ; k3 = 5 \(\Rightarrow\) Trong khoảng giữa có 1 vị trí trùng nhau.
Vị trí 3: k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_3:\) \(\frac{k_1}{k_3}=\frac{\lambda_3}{\lambda_1}=\frac{3}{2}=\frac{6}{4}=\frac{9}{6}=\frac{12}{8}=\frac{15}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k3 = 10 thì có tất cả 6 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 3 ; k3 = 2
Vị trí 3: k1 = 6 ; k3 = 4
Vị trí 4: k1 = 9 ; k3 = 6 \(\Rightarrow\) Trong khoảng giữa có 4 vị trí trùng nhau.
Vị trí 5: k1 = 12 ; k3 = 8
Vị trí 6: k1 = 15 ; k3 = 10
Vậy tất cả có 2 + 1 +4 = 7 vị trí trùng nhau của các bức xạ.
Số VS quan sát được = Tổng số VS tính toán – Số vị trí trùng nhau = 34 – 7 = 27 vân sáng.
\(\rightarrow D\)

Khoảng cách giữa 2 vân sáng gần nhau nhất cùng màu với vân trung tâm: \(x_T=k_1i_1=k_2i_2\)(1)
\(\Rightarrow k_1\lambda_1=k_2\lambda_2\Rightarrow\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,6}{0,48}=\frac{5}{4}\)
\(\Rightarrow\begin{cases}k_1=5\\k_2=4\end{cases}\)
Thay vào (1) \(x_T=5i_1=4i_2\)
Như vậy tại vị trí 2 vân trùng nhau kể từ vân trung tâm có vân bậc 5 của \(\lambda_1\) và bậc 4 của \(\lambda_2\)
Do đó, giữa 2 vân sáng cùng màu vân trung tâm có: 4 vân sáng λ1 và 3 vân sáng λ2.
Đáp án A.

\(x_s= k\frac{\lambda D}{a}.\)
\(d_2-d_1 = \frac{x_sa}{D}= k\lambda\)
=>\(k= \frac{d_2-d_1}{\lambda}=\frac{1,5.10^{-6}}{\lambda}.(1)\)
Thay các giá trị của bước sóng \(\lambda\)1, \(\lambda\)2,\(\lambda\)3 vào biểu thức (1) làm sao mà ra số nguyên thì đó chính là vân sáng của bước sóng đó.

720nm = 0,72 μm
giữa 2 vân sáng gần nhau nhất và cùng màu vs vân sáng trung tâm có 8 vân sáng màu lục => Tại vị trí trùng đó là VS bậc 9 của λlục
Tại VT trùng nhau: x_kđỏ = x_9lục
<=> kđỏ.λđỏ = 9.λlục
<=> kđỏ/9 = λlục/λđỏ = λ/0,72
=> λ = (0,72.kđỏ)/9 = 0,08.kđỏ (*)
0,5 ≤ λ = 0,08.kđỏ ≤ 0,575 μm
6,25 ≤ kđỏ ≤ 7,1875
=> kđỏ = 7
thế vào λ = 0,56 (μm) = 560nm