Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: k 1 k 2 = λ 2 λ 1 = 0 , 4 0 , 6 = 2 3 = 2 n 3 n ⇒ k 1 = 2 n
Vị trí vân sáng trùng: x s t = k 1 i 1 = k 2 i 2 ⇒ x s t = 2 n i 1
Số vân sáng trùng trong khoảng giữa 2 vân bậc 7 của λ 1 = λ thỏa điều kiện:
− 7 i 1 < x s t < 7 i 1 ⇔ − 7 i 1 < 2 n i 1 < 7 i 1 ⇔ − 3 , 5 < n < 3 , 5 ⇒

Chọn đáp án D.
Ba vân trùng nhau nên ta có x1 = x2 = x3
![]()
![]()
![]()
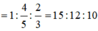
Vậy tại vị trí trùng nhau đầu tiên của 3 bức xạ tính từ vân trung tâm thì đó là vân sáng bậc 15 của λ1, vân sáng bậc 12 của λ2 và vân sáng bậc 10 của λ3.
Xét các vị trí trùng nhau của λ1 và λ2:
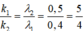
Vậy với các giá trị của k1 chia hết cho 5 thì là giá trị của k ứng với vị trí trùng nhau của λ1 và λ2 => có 2 vân trùng.
Xét các vị trí trùng nhau của λ1 và λ3:
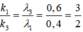
Vậy với các giá trị của k1 chia hết cho 3 thì là giá trị của k ứng với vị trí trùng nhau của λ1 và λ3 => có 4 vân trùng.
Xét các vị trí trùng nhau của λ3 và λ2:
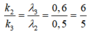
Vậy với các giá trị của k2 chia hết cho 6 thì là giá trị của k ứng với vị trí trùng nhau của λ3 và λ2 => có 1 vân trùng.
Vậy số vân sáng quan sát được trong khoảng giữa hai vân trùng nhau của 3 bức xạ là: 14 + 11 + 9 – 2 – 4 – 1 = 27 vân sáng.

Đáp án A
+ Ta chú ý rằng có (n+1) vân sáng liên tiếp thì cách nhau d = n i
Suy ra, nếu ta xét d = i 123 = n x i x thì có n + 1 vân của bức xạ λ x khoảng ở giữa có n + 1 − 1 − 1 = n − 1 vân (vì không xét 2 vân ở mút)
+ Từ đó ta thiết lập:
i 123 = 12 i 1 = 9 i 2 = 8 i 3 = 3 i 12 = i 23 = 4 i 13
Giải thích lập tỷ số
i 1 i 2 = λ 1 λ 2 = 3 4 ⇒ i 12 = 4 i 1 = 3 i 2 ( 1 ) i 2 i 3 = λ 2 λ 3 = 8 9 ⇒ i 23 = 9 i 2 = 8 i 3 ( 2 ) i 3 i 1 = λ 3 λ 1 = 3 2 ⇒ i 31 = 2 i 3 = 3 i 1 ( 3 ) i 12 i 3 = 4 i 1 3 i 1 / 2 = 8 3 ⇒ i 123 = 3 i 12 = 8 i 3 ( 4 )
Từ (1); (2); (3) ta được tỷ lệ trên
Số vân sáng đơn sắc cần tìm là N = N 1 + N 2 + N 3 − 2 N 12 + N 23 + N 13 = 11 + 8 + 7 − 2 2 + 0 + 3 = 16