Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Số cách chọn ngẫu nhiên 2 lá phiếu là: C 9 2 = 36 (cách)
Các cặp số có tổng là một số lẻ lớn hơn hoặc bằng 15 là: (9;8); (9;6); (8;7). Xác suất để tổng của hai số ghi trên hai lá phiếu rút được là một số lẻ lớn hơn hoặc bằng 15 là: 3 36 = 1 12

Đáp án A
Tổng số phiếu trong hộp là 24. Gọi Ω là không gian mẫu.
* Lấy ngẫu nhiên 4 phiếu trong hộp ta có ![]() cách lấy hay
cách lấy hay ![]()
Gọi A là biến cố lấy được các phiếu có đủ cả 3 loại.
Ta có các trường hợp sau:
+) 2 đỏ, 1 vàng và 1 xanh: có![]() cách
cách
+) 1 đỏ, 2 vàng và 1 xanh: có ![]() cách
cách
+) 1 đỏ, 1 vàng và 2 xanh: có ![]() cách
cách
Do đó, ![]()
Vậy, xác suất biến cố A là
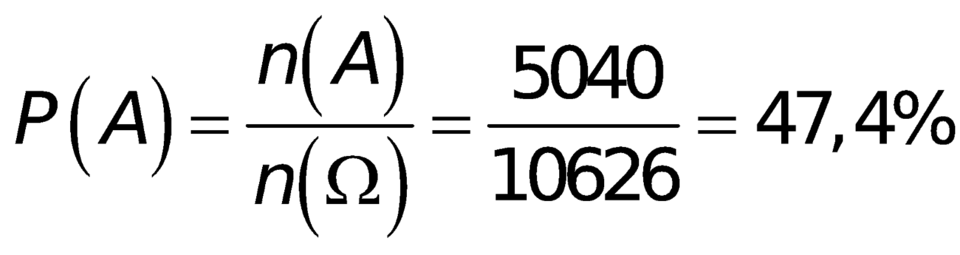

- Có 5 cách chọn chữ số hàng trăm.
- Có 5 cách chọn chữ số hàng chục.
- Có 4 cách chọn chữ số hàng đơn vị.
Số số được tạo thành là:
\(5.5.4=100\) (số)
Tuy nhiên trong 100 số này đã bị mất đi 1 số số chẵn:
| 012 | 013 | 014 | 015 |
| 021 | 023 | 024 | 025 |
| 031 | 032 | 034 | 035 |
| 041 | 042 | 043 | 045 |
| 051 | 052 | 053 | 054 |
Vậy số số lẻ hơn số số chẵn là 8 số.
Có số số chẵn là:
\(\left(100-8\right):2=46\) (số)
Có số số lẻ là :
\(100-46=54\) (số)
Nếu coi 100 số là 100 %.
Xác xuất chọn được số chẵn ở lần chọn đầu là:
\(46:100.100=46\%\)
Xác xuất chọn được số chẵn ở lần chọn thứ 2 (nếu lần ko trúng) là:
\(46:99.100\approx46,5\)

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

Đáp án A
Rút ngẫu nhiên 2 thẻ trong 9 thẻ có C 9 2 cách ⇒ n ( Ω ) = C 9 2
Gọi X là biến cố “hai thẻ rút được có tích 2 số ghi trên 2 thẻ là số lẻ”
Khi đó 2 thẻ rút ra đều phải đưuọc đánh số lẻ => có C 5 2 cách => n ( X ) = C 5 2 .
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = C 5 2 C 9 2 = 5 18 .

Đáp án D
Có 2 trường hợp sau:
+) 1 thẻ ghi số chẵn, 1 thẻ ghi số lẻ, suy ra có C 4 1 . C 5 1 = 20 cách rút.
+) 2 thẻ ghi số chẵn, suy ra có C 4 2 = 6 cách rút.
Suy ra xác suất bằng 20 + 6 C 9 2 = 13 18 .

Xác suất lấy ra quả cầu không có số 1 hoặc số 5 từ túi đầu tiên: \(\frac{8}{{10}} = \frac{4}{5}\)
Xác suất lấy được quả cầu không có số 1 hoặc số 5 từ túi thứ hai là: \(\frac{8}{{10}} = \frac{4}{5}\)
Vì lấy ngẫu nhiên từ hai túi khác nhau một quả cầu nên hai biến cố quả cầu lấy ra mỗi túi không có số 1 hoặc số 5 là độc lập.
Vậy xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5 là: \(\frac{4}{5}.\frac{4}{5} = \frac{{16}}{{25}}\)
Đáp án C
Số cách rút hai lá phiếu là C 9 2
Gọi p là biến cố hai lá phiếu rút được có tổng lẻ lớn hơn hoặc bằng 15