K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

13 tháng 8 2021
Ta có : 2 quả táo + 2 quả cam = 6 $
- 4 quả táo + 3 quả cam = 10 $
Bằng với : 4 quả táo + 4 quả cam = 12 $
- 4 quả táo + 3 quả cam = 10$
= 1 quả cam = 2 $
Vậy một quả táo có giá : 10 - ( 2 x 3 ) :4 = 1$

NA
25 tháng 12 2021
khó nhìn là do iem dịch ra ms vậy á:< bản gốc là chữ tiếng anh mà

3 tháng 12 2015
a/3 + 20 + (a/3) : (3/4) = a
a/3 + 4a/9 + 20 = a
a - (7a /9) = 20
2a /9 = 20
a = 90
Số cam = 90/3 = 30
Số táo: 90 - 20 - 30 = 40
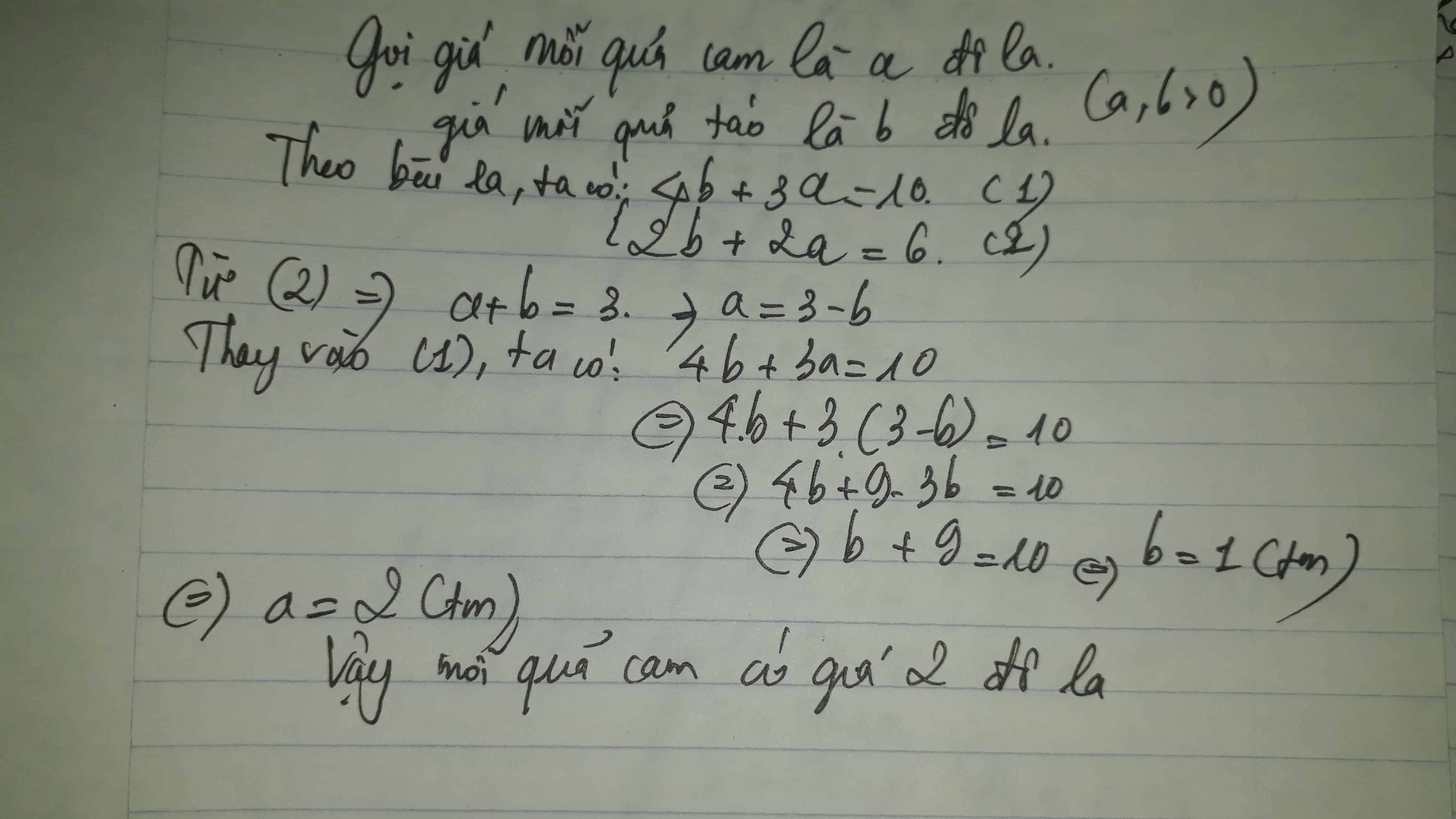


Lời giải:
Gọi số quả táo, cam, kiwi lần lượt là $a,b,c$ với $a,b,c\in\mathbb{N}^*$. Theo bài ra ta có:
$a+b+c=30$
$3a+4b+6c=169$
Cần tìm $c$ thỏa mãn các điều kiện trên mà vẫn đảm bảo $c$ lớn nhất.
$a\geq 1; b\geq 1$
$6c=169-3a-4b\leq 169-3.1-4.1=162$
$\Rightarrow c\leq 27$
Nếu $c=27$ thì:
$a+b=3$
$3a+4b=7$
$\Rightarrow 3(3-b)+4b=7\Rightarrow b=-2$ (vô lý)
Nếu $c=26$ thì:
$a+b=4$
$3a+4b=13$
$\Rightarrow 3(4-b)+4b=13$
$\Rightarrow b=1; a=3$ (thỏa mãn)
Vậy số quả kiwi nhiều nhất là $26$ quả.
giúp mik với ạ