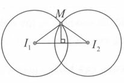
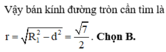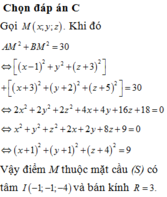Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi M x ; y ; z ⇒ A M → = x − 1 ; y ; z + 3 , B M → = x + 3 ; y + 2 ; z + 5
Khi đó A M 2 + B M 2 = 30 ⇔ x − 1 2 + y 2 + z + 3 2 + x + 3 2 + y + 2 2 + z + 5 2 = 30
⇔ x − 1 2 + y + 1 2 + z + 4 2 = 9 ⇒ M ∈ S có tâm I − 1 ; − 1 ; − 4 , R = 3

Đáp án A
Vì M ∈ d nên M t + 3 ; − t − 2 ; 2 t + 1 , t ∈ ℝ
Đường thẳng Δ có vtcp u Δ → = − 1 ; 2 ; − 3 .
Đường thẳng d ' : qua M t + 3 ; − t − 2 ; 2 t + 1 vtcp u d ' → = u Δ → = − 1 ; 2 ; − 3
⇒ d ' : x − t + 3 − 1 = y + t + 2 2 = z − 2 t + 1 − 3
M’ là hình chiếu song song của M trên (P)
⇒ M ' = d ' ∩ P ⇒ M ' 5 9 t + 2 ; − 1 9 t ; 2 3 t − 2 .
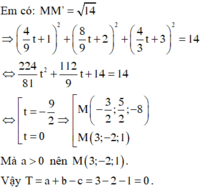

Đáp án A

Thay tọa độ điểm A, B vào biểu thức vế trái của phương trình
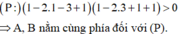
Gọi A'(x';y';z') đối xứng A qua (P), K là trung điểm của AA'.
Mặt phẳng (P) có vectơ pháp tuyến n P → = 1 ; − 2 ; − 1 . Khi đó:
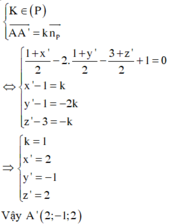
MA+MB đạt giá trị nhỏ nhất khi M ≡ I là giao điểm của A'B và (P).
Điểm I(x;y;z) thỏa mãn
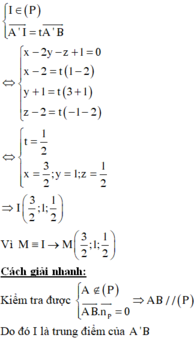
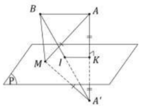

Chọn B
Đặt M(x;y;z). Lập hệ 3 phương trình ba ẩn x,y,z từ phương trình mặt phẳng (P) và điều kiện MA=MB, MA=MC