Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Phân tích.
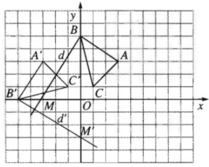
- Ta thấy A thuộc đường phân giác trong góc A:x-3y+5=0 , giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.




Đáp án B
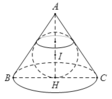
Mặt cầu nội tiếp hình nón đề cho có 1 đường trong lớn nội tiếp tam giác đều (cạnh a)
Nên mặt cầu đó có bán kính 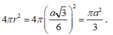
![]()
Vậy diện tích mặt cầu cần tìm là V = 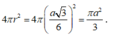

d:x+y-2=0 A B C I E(3;1) D(-2;1) P(2;1)
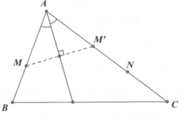
Ta dễ có tứ giác ABDE nội tiếp đường tròn đường kính AB => ^CDE = ^BAE
Lại có ^BAE = ^CAD (= 900 - ^ACB), suy ra ^CDE = ^CAD = 900 - ^ACD => DE vuông góc AC
Thấy D,E,P cùng có tung độ bằng 1 => D,E,P thẳng hàng, vì P thuộc AC nên DE vuông góc với AC tại P
Đường thẳng AC: đi qua P(2;1), VTPT \(\overrightarrow{DE}=\left(5;0\right)\) \(\Rightarrow AC:x-2=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\x+y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=0\end{cases}}\Rightarrow A\left(2;0\right)\)
Đường thẳng BC: đi qua \(D\left(-2;1\right)\),VTPT \(\overrightarrow{DA}=\left(4;-1\right)\Rightarrow BC:4x-y+9=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\4x-y+9=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=17\end{cases}\Rightarrow C\left(2;17\right)}\)
Đường thẳng BE: đi qua \(E\left(3;1\right)\), VTPT \(\overrightarrow{AE}=\left(1;1\right)\Rightarrow BE:x+y-4=0\)
Xét hệ: \(\hept{\begin{cases}4x-y+9=0\\x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=5\end{cases}}\Rightarrow B\left(-1;5\right)\)
Vậy \(A\left(2;0\right),B\left(-1;5\right),C\left(2;17\right)\).