Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

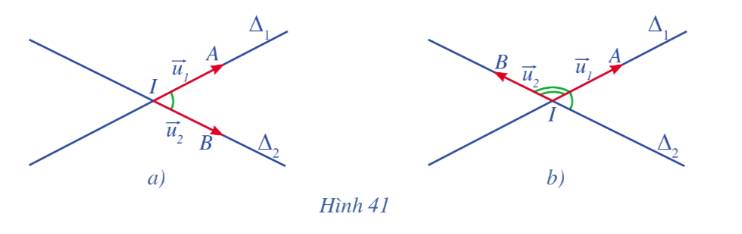
a) Độ lớn của góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \),\(\overrightarrow {IB} \)có thể bẳng nhau hoặc bù nhau.
b) Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \le {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \ge 0\).
Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) > {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = {180^o} - \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = - \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) < 0\).
Vậy ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\)

Ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}.\)

Dựa vào hình vẽ ta có
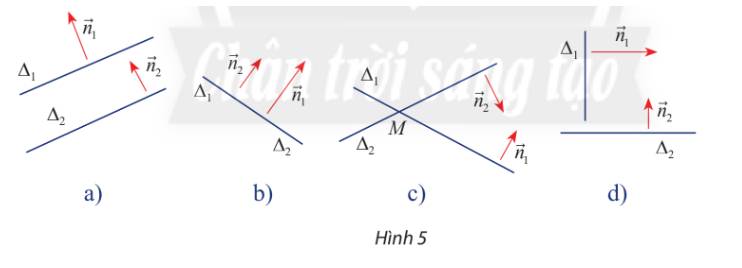
a) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cùng phương thì hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) song song
b) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) không cùng phương thì hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) cắt nhau
c) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc thì hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) vuông góc

a) Góc \(\varphi \) và góc \(\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\) có thể bằng nhau hoặc bù nhau.
b) Do góc \(\varphi \) và góc \(\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\) có thể bằng nhau hoặc bù nhau nên \(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\)

+) Từ phương trình \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_1}} \) là \(\left( {{a_1};{b_1}} \right)\)
+) Từ phương trình \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_2}} \) là \(\left( {{a_2};{b_2}} \right)\)
+) \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\)

a) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {1;3} \right),\overrightarrow {{n_2}} = \left( {1; - 2} \right)\)
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {1.1 + 3.( - 2)} \right|}}{{\sqrt {{1^2} + {3^2}} \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} \approx 0,93 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) \approx 22^\circ 8'\)
b) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {4; - 2} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {4.2 + ( - 2).( - 1)} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 1 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = 0^\circ \)
c) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {2; - 1} \right),\overrightarrow {{n_2}} = \left( {1;2} \right)\)
Ta có \({a_1}{a_2} + {b_1}{b_2} = 2.1 + ( - 1).2 = 0\)
Suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ \)

a) Tọa độ giao điểm của hai đường thẳng \({\Delta _1};{\Delta _2}\)là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}\sqrt 3 x + y - 4 = 0\\x + \sqrt 3 y - 2\sqrt 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \sqrt 3 \\y = 1\end{array} \right.\)
b) Ta có: \(\cos \left( {{\Delta _1};{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{2\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{2} \Rightarrow \left( {{\Delta _1};{\Delta _2}} \right) = {30^o}\)
Vậy số đo góc giữa hai đường thẳng \({\Delta _1};{\Delta _2}\) là \({30^o}\).

a) - Ta có: \(\overrightarrow {{u_1}} = \left( {3\sqrt 3 ;3} \right);\overrightarrow {{u_2}} = \left( {1 ;0} \right) \Rightarrow \cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {3\sqrt 3 .1 + 3.0} \right|}}{{\sqrt {{{\left( {3\sqrt 3 } \right)}^2} + {3^2}} .\sqrt {{1^2} + {0^2}} }} = \frac{{\sqrt 3 }}{2}.\)
- Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {30^o}\)
b) – Ta có\(\overrightarrow {{n_1}} = \left( {2; - 1} \right);\overrightarrow {{n_2}} = \left( { - 1 ;3} \right) \Rightarrow \cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.\left( { - 1} \right) + \left( { - 1} \right).3} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{{\left( 1 \right)}^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2}.\)
- Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {45^o}\)

Nhận xét
• Nếu ủ là một vectơ chỉ phương của A thì \(k\overrightarrow u \) (\(k \ne 0\))cũng là một vectơ chỉ phương của A.
• Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ chỉ phương của đường thẳng đó.

Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Khi đó:
a) \({\Delta _1}\) cắt \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) không cùng phương.
b) \({\Delta _1}\) song song với \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) cùng phương và có một điểm thuộc một đường thẳng mà không thuộc đường thẳng còn lại.
c) \({\Delta _1}\) trùng với \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) cùng phương và có một điểm thuộc cả hai đường thẳng đó.