Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0

Gọi M′(x′;y′) ∈ d′ là ảnh của M(x,y) ∈ d qua phép tịnh tiến theo vecto v → ( 2 ; 3 )
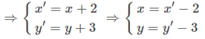
Do M(x,y) ∈ d nên
3x − 5y + 3 = 0
⇒ 3(x′−2) − 5(y′−3) + 3 = 0
⇔ 3x′ − 5y′ + 12 = 0 (d′)
Vậy M′(x′;y′) ∈ d′: 3x′ − 5y′ + 12 = 0

Gọi d 1 là ảnh của d qua phép quay tâm 0 góc 90 o . Vì d chứa tâm quay O nên d 1 cũng chứa O. Ngoài ra d 1 vuông góc với d nên d 1 có phương trinh: 9x + 2y = 0.
Gọi d' là ảnh của d 1 qua phép tịnh tiến vectơ v. Khi đó phương trình của d' có dạng x + 2y + C = 0. Vì d' chứa O′(3;1) là ảnh của O qua phép tịnh tiến vectơ v nên 3 + 2 + C = 0 từ đó C = -5. Vậy phương trình của d' là x + 2y – 5 = 0.

Lời giải:
Xét $A(x,y)\in d$ và $M'(x',y')=T_{\overrightarrow{v}}$. Ta có:
\(\left\{\begin{matrix} x'-x=-2\\ y'-y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=x'+2\\ y=y'-5\end{matrix}\right.\)
Thay vào $(d)$:
$x'+2+y'-5+3=0$
$\Leftrightarrow x'+y'=0$ (đây là ptđt $d'$ cần tìm)
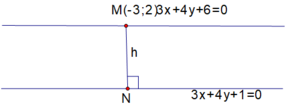

Gọi d' là ảnh của d qua phép tịnh tiến \(\overrightarrow{v}\)
Gọi \(A\left(x_A;y_A\right)\) là 1 điểm bất kì thuộc d \(\Rightarrow x_A-3y_A+5=0\) (1)
Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)
Ta có: \(\left\{{}\begin{matrix}x_{A'}=x_A+1\\y_{A'}=y_A+3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_A=x_{A'}-1\\y_A=y_{A'}-3\end{matrix}\right.\) thế vào (1):
\(x_{A'}-1-3\left(y_{A'}-3\right)+5=0\)
\(\Leftrightarrow x_{A'}-3y_{A'}+13=0\)
Vậy pt d' có dạng: \(x-3y+13=0\)