

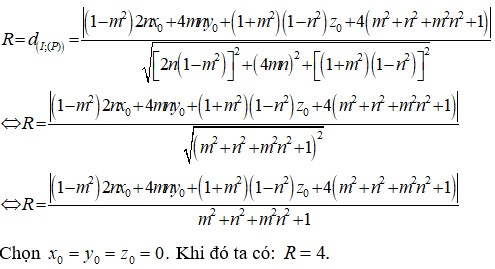
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


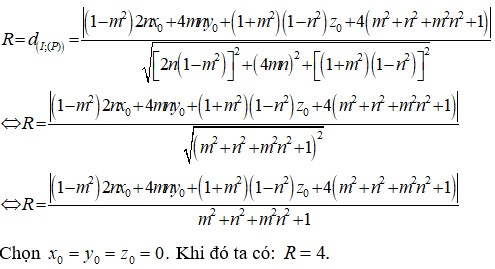

Đáp án D.
Gọi I(a,b,c) là tâm mặt cầu cố định đó. Rõ ràng d(I,(P)) = R không đối với mọi m , n ∈ ℝ .
Với m = 1 ⇒ d I , P = 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
Với m = - 1 ⇒ d I , P = - 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
⇒ 2 n b + 1 - n 2 c + 4 n 2 + 1 = - 2 n b + 1 - n 2 c + 4 n 2 + 1 ⇔ [ b = 0 1 - n 2 c + 4 n 2 + 1 = 0
Rõ ràng 1 - n 2 c + 4 n 2 + 1 = 0 không thể xảy ra với mọi n ∈ ℝ suy ra b = 0
Với m = n = 1 ⇒ d I , P = b + 4 = R = 4 .

Đáp án D
Hướng giải: Ta sẽ đi tìm 1 mặt phẳng song song với (P), đồng thời tiếp xúc với mặt cầu. Lúc này, khoảng cách giữa 2 mặt phẳng này chính là 2 lần bán kính mặt cầu.
Do (P) luôn tiếp xúc với 1 mặt cầu cố định => Ta chọn tùy ý m, n để được 2 mặt phẳng song song
+ Chọn m=1,n=1 =>4y+16=0 => y = - 4 ( α 1 )
+ Chọn m=-1,n=1 => -4y+16=0 => y=4 ( α 2 )
d ( ( α 1 ) , ( α 2 ) ) = 8 = > r = 4