Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Xét mặt cầu:
S : x − 2 2 + y − 1 2 + z 2 = 9 ⇒ I 2 ; 1 ; 0 ; R = 3
Khoảng cách từ tâm I đến mặt phẳng (P) là d I ; P = 2 m + 3 m 2 + 5
Theo giả thiết, Mặt phẳng (P) cắt mặt cầu S : x − 2 2 + y − 1 2 + z 2 = 9 theo một đường tròn có bán kính bằng r = 2
Suy ra:
d 2 + r 2 = R 2 ⇔ 2 m + 3 2 m 2 + 5 + 2 2 = 3 2 ⇔ m 2 − 12 m + 16 = 0 ⇔ m = 6 ± 2 5

Chọn B
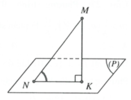
Gọi tâm mặt cầu là I(x;0;0). Tìm x từ điều kiện vecto Im và vecto n cùng phương, với vecto n là VTPT của mặt phẳng (P).





Đáp án D.
Gọi I(a,b,c) là tâm mặt cầu cố định đó. Rõ ràng d(I,(P)) = R không đối với mọi m , n ∈ ℝ .
Với m = 1 ⇒ d I , P = 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
Với m = - 1 ⇒ d I , P = - 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
⇒ 2 n b + 1 - n 2 c + 4 n 2 + 1 = - 2 n b + 1 - n 2 c + 4 n 2 + 1 ⇔ [ b = 0 1 - n 2 c + 4 n 2 + 1 = 0
Rõ ràng 1 - n 2 c + 4 n 2 + 1 = 0 không thể xảy ra với mọi n ∈ ℝ suy ra b = 0
Với m = n = 1 ⇒ d I , P = b + 4 = R = 4 .