Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Cách 1 (Véc tơ đơn vị). Ta có
![]()
=> Tam giác OAB vuông tại O
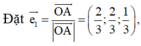
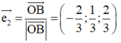

Gọi H, E là các tiếp điểm của đường tròn nội tiếp với các cạnh OA, OB.
Ta có
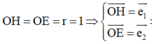
![]()
Cách 2. Kẻ phân giác OE suy ra
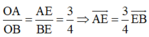
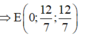
Gọi I là tâm đường tròn nội tiếp tam giác OAB
![]()
Tam giác OAB vuông tại O, có bán kính đường tròn nội tiếp r =1 ⇒ I O = 2
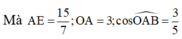
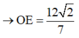
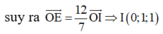

Đáp án A
Phương pháp giải:
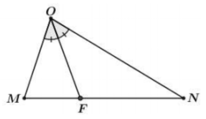
Tìm tọa độ tâm đường tròn ngoại tiếp tam giác OMN bằng tính chất đường phân giác
![]()
Vectơ chỉ phương của
![]()
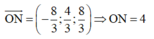
Kẻ phân giác OF (F ∈ MN) ta có:
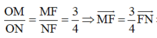
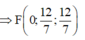
Gọi I là tâm đường tròn nội tiếp tam giác OMN
![]()
Tam giác OMN vuông tại O, có bán kính đường tròn nội tiếp r=2 => OI = 2
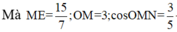

Phương trình đường thẳng ∆ là
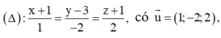
đi qua I(0;1;1)
Khoảng cách từ E đến đường thẳng ∆ là
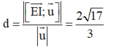

Đáp án A
Dễ thấy tọa độ trung điểm của đoạn thẳng AB là điểm

Đáp án C.
Gọi I(a,b,c) là tâm mặt cầu đi qua 4 điểm A(2;3;-1), B(-1;2;1), C(2;5;1), D(3,4,5)
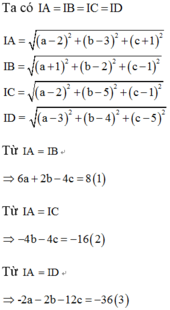


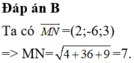
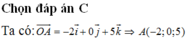

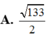
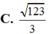
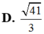
Đáp án A