Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi phương trình đường thẳng ∆ là
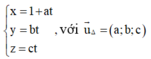
Vì ∆ nằm trong mặt phẳng (P)
![]()
Góc giữa hai đường thẳng ∆ và Oz là
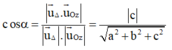
Ta có
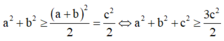
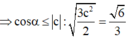
Khi cos α lớn nhất ⇒ α nhỏ nhất và bằng a r cos 6 3 . Xảy ra khi b = 2 c = 2 a
Do đó, phương trình đường thẳng ∆ là
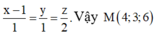

Chọn A
Gọi I (a;b;c)
Ta có IA=IO=R ó hình chiếu của I lên OA là trung điểm 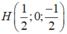 của OA.
của OA.
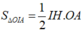
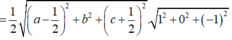
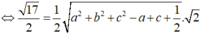
![]()
![]()
Theo bài ra ta có:
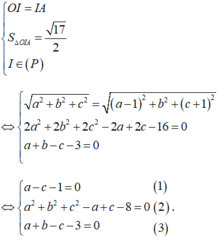
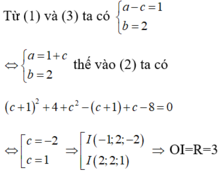

Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
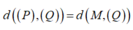
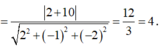
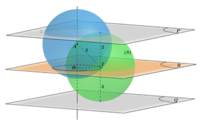
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
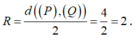
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
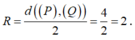
![]()
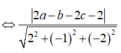
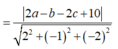
![]()
![]()
![]()
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
![]()
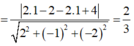
![]()
do đó tam giác AHI vuông tại H nên
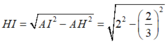
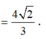
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
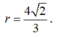

Chọn A
Gọi ![]() là một vec tơ pháp tuyến của mặt phẳng (P).
là một vec tơ pháp tuyến của mặt phẳng (P).
Theo đề bài ta có mặt phẳng (P) vuông góc với mặt phẳng (α): x-y+z-4=0 nên ta có phương trình a-b+c=0 ó b=a+c ![]()
Phương trình mặt phẳng (P) đi qua A(0;1;2) và có véc tơ pháp tuyến là ax+ (a+c) (y-1)+c (z-2) =0
Khoảng cách từ tâm I (3;1;2) đến mặt phẳng (P) là 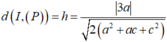
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu (S) và mặt phẳng (P) ta có r²=16-h² ; r nhỏ nhất khi h lớn nhất.
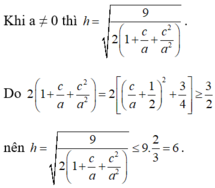
Dấu “=” xảy ra khi a = -2c. => một véc tơ pháp tuyến là ![]() => phương trình mặt phẳng (P) là 2x+y-z+1=0.
=> phương trình mặt phẳng (P) là 2x+y-z+1=0.
Vậy tọa độ giao điểm M của (P) và trục x'Ox là: 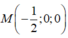




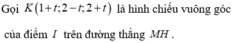
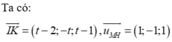
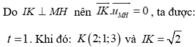
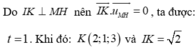

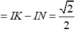
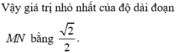


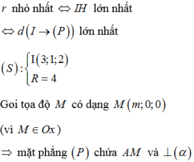

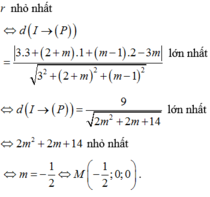

Mặt cầu (S) có tâm I(2;-1;2), mặt phẳng (P) có VTPT\(\overrightarrow{n}\)=(1;-1;2). Gọi điểm C(x;y;z) ta có C∈ (S) nên \(\left(x-2\right)^2+\left(y-1\right)^2+\left(z-2\right)^2=4\left(1\right)\)
Do CD là đường kính của mặt cầu (S) nên I là trung điểm của CD
=> D(4-x; -y -2; 4-z)
Mà theo đề có CD//(P) nên
\(\overrightarrow{IC}\perp\overrightarrow{n}\Leftrightarrow\overrightarrow{IC}.\overrightarrow{n}=0\) <=> \(x-2-\left(y+1\right)+2\left(z-2\right)=0\left(2\right)\)
Ta có: \(\overrightarrow{AB}=\left(1;-1;-1\right);\overrightarrow{AC}=\left(x;y-1;z-1\right);\overrightarrow{AD}=\left(4-x;y-3;3-z\right)\)
\(\left|\overrightarrow{AC;}\overrightarrow{AD}\right|=\left(2y+4z-6;-2x+4z-4;-4x-y+4\right)\)
\(\overrightarrow{AB}\left|\overrightarrow{AC};\overrightarrow{AD}\right|=2x+4z-6+\left(-1\right)\left(-2x+4z-4\right)+\left(-1\right)\left(-4x-4y+4\right)=6x+6y-6\)
Thể tích khối tứ diện ABCD là:
V = \(\dfrac{1}{6}\left|\overrightarrow{AB}\left[\overrightarrow{AC};\overrightarrow{AD}\right]\right|=\left|x+y-1\right|\)
Đặt : \(\left\{{}\begin{matrix}x-2=a\\y+1=b\\z-2=c\end{matrix}\right.\)
Từ (1) và (2) có hệ : \(\left\{{}\begin{matrix}a^2+b^2+c^2=4\\a-b+2c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-b=-2c\\ab=\dfrac{4-5c^2}{2}\end{matrix}\right.\)
V=|x+y-1| = |x-2+y +1| = |a+b| = \(\sqrt{\left(a-b\right)^2+4ab}\) = \(\sqrt{4c^2+2\left(4-5c^2\right)}=\sqrt{8-6c^2}\le2\sqrt{2}\)
Vậy GTLN của V là 2\(\sqrt{2}\) khi
\(\left\{{}\begin{matrix}z-2=0\\x-2=0\\\left(x-2\right)^2+\left(y-1\right)^2+\left(z-2\right)^2=4\end{matrix}\right.\) <=>\(\left\{{}\begin{matrix}x=2+\sqrt{2};y=-1+\sqrt{2};z=2\\x=2-\sqrt{2};y=-1-\sqrt{2};z=2\end{matrix}\right.\)