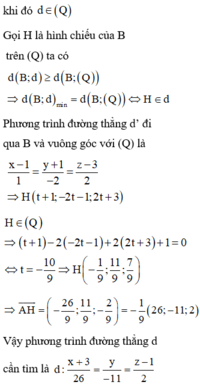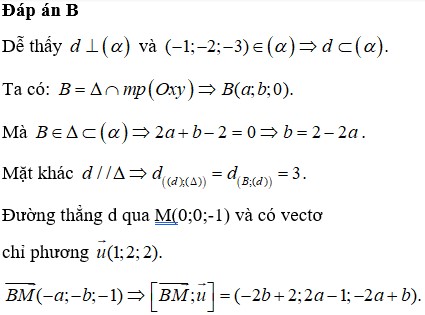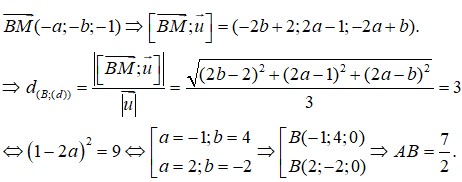Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
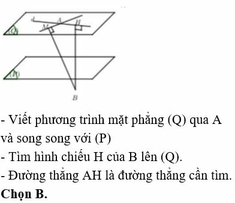
Gọi (Q) là mặt phẳng đi qua A và song song với mặt phẳng (P). Khi đó phương trình của mặt phẳng (Q) là
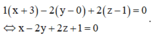
Gọi H là hình chiếu của điểm B lên mặt phẳng (Q), khi đó đường thẳng BH đi qua B(1;-1;3)
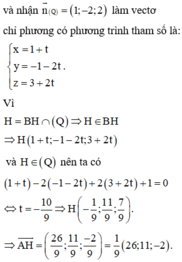
Gọi K là hình chiếu của B lên đường thẳng d, khi đó ta có


Chọn C
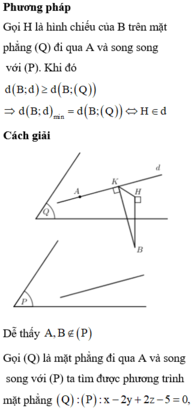
Phương pháp:
Cách giải:
Gọi d là đường thẳng cần tìm.

Vậy khoảng cách từ B đến (d) nhỏ nhất khi H trùng I. vậy phương trình (d) qua A và H là:
x + 3 26 = y 11 = z - 1 - 2

Chọn A
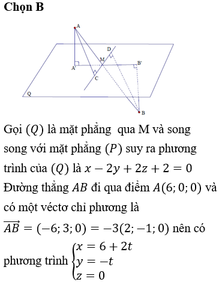
Khoảng cách từ B đến đường thẳng d là lớn nhất nếu AB vuông góc với d.
Đường thẳng d qua A và nhận vecto chỉ phương là A B → ; n → với n ⇀ là vecto pháp tuyến của mặt phẳng (P).

2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ

Đáp án B
Cách giải: A B → = - 1 ; - 2 ; 3
d:
x
-
2
1
=
y
-
1
-
2
=
z
-
1
2
có 1 VTCP
v
→
1
;
-
2
;
2
là một VTCP của ∆
∆ là đường thẳng qua A, vuông góc với d => ∆
⊂
(α) mặt phẳng qua A và vuông góc d
Phương trình mặt phẳng (α): 1(x – 3) – 2(y – 2) + 2(z – 1) = 0 ó x – 2y + 2z – 1 = 0
Khi đó, ![]() khi và chỉ khi ∆ đi qua hình chiếu H của B lên (α)
khi và chỉ khi ∆ đi qua hình chiếu H của B lên (α)
*) Tìm tọa độ điểm H:
Đường thẳng BH đi qua B(2;0;4) và có VTCP là VTPT của (α) có phương trình:

![]()
![]()
=> ![]()
<=> ![]()
∆ đi qua A(3;2;1), H(1;2;2) có VTCP H A → = 2 ; 0 ; - 1 = u → 2 ; b ; c ; u → = 5