Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B.
Vì 4 điểm không đồng phẳng tạo thành một tứ diện mà tứ diện có 4 mặt.
Đáp án B
A B → - 1 ; 2 ; 0 , A D → 1 ; - 2 ; 0 , A B → = - A D → ⇒ A , B , D thẳng hàng
Cứ 3 điểm không thẳng hàng cho ta một mặt phẳng
Số cách chọn 3 trong 5 điểm trên là C 5 3 = 10
A,B,D thẳng hàng nên qua 3 điểm này không xác định được mặt phẳng
Số cách chọn 2 trong và điểm A,B,D và 1 điểm trong O và C là: C 3 2 . C 2 1 = 6
Nếu chọn 2 trong 3 điểm A,B,D kết hợp cùng hai điểm còn lại sẽ ra một số mặt phẳng trùng nhau. Nên trường hợp này ta chỉ xác định được 2 mặt phẳng phân biệt
Vậy số mặt phẳng phân biệt đi qua 3 điểm O,A,B,C,D là: 10-1-6+2=5
Đáp án B
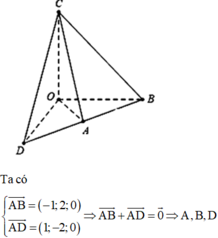
Ta có
A
B
→
=
-
1
;
2
;
0
A
D
→
=
1
;
-
2
;
0
⇒
A
B
→
+
A
D
→
=
0
⇒
A
,
B
,
D
thẳng hàng
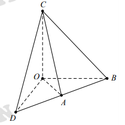
Do đó, 5 điểm O, A, B, C, D tạo thành tứ diện như hình vẽ bên
Vậy có tất cả 5 mặt phẳng cần tìm đó là:
+ Mặt phẳng (OAC) đi qua 3 điểm O, A, C.
+ Bốn mặt phẳng là các mặt bên của tứ diện O.BCD đi qua 3 điểm trong 5 điểm O, A, B, C, D.
Đáp án B
A B → ( − 1 ; 2 ; 0 ) , A D → ( 1 ; − 2 ; 0 ) , A B → = − A D → ⇒ A , B , D thẳng hàng
Cứ 3 điểm không thẳng hàng cho ta một mặt phẳng
Số cách chọn 3 trong 5 điểm trên là C 5 3 = 10
A,B,D thẳng hàng nên qua 3 điểm này không xác định được mặt phẳng
Số cách chọn 2 trong và điểm A,B,D và 1 điểm trong O và C là: C 3 2 . C 2 1 = 6
Nếu chọn 2 trong 3 điểm A,B,D kết hợp cùng hai điểm còn lại sẽ ra một số mặt phẳng trùng nhau. Nên trường hợp này ta chỉ xác định được 2 mặt phẳng phân biệt
Vậy số mặt phẳng phân biệt đi qua 3 điểm O,A,B,C,D là: 10 - 1 - 6 + 2 = 5
Đáp án D
Số cách chọn ra 3 điểm từ 2n điểm đã cho là C 2 n 3 suy ra số mặt phẳng được tạo ra là C 2 n 3 .
Do trong 2n điểm đã cho có n điểm đồng phẳng nên có C n 3 mặt phẳng trùng nhau.
Suy ra số mặt phẳng được tạo thành từ 2n điểm đã cho là C 2 n 3 − C n 3 + 1 .
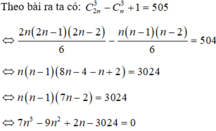
Đáp án A
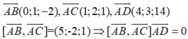
⇒ A B → , A C → , A D → đồng phẳng suy ra tồn tại vô số mặt phẳng cách đều 4 điểm trên
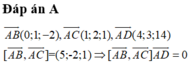
⇒ A B → , A C → , A D → đồng phẳng suy ra tồn tại vô số mặt phẳng cách đều 4 điểm trên
Đáp án B
Cứ ba điểm không thẳng hàng xác định được một mặt phẳng. Với bốn điểm không đồng phẳng có thể xác định được C 4 3 = 4 mặt phẳng. Có thể thấy đáp án bài này qua hình tứ diện.