Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
√3,2 √1,28 √1,92 v O M N
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)

Vận tốc cực đại: \(v_{max}=\sqrt{\dfrac{2W_{đmax}}{m}}=\sqrt{\dfrac{2.0,1}{0,2}}=1m/s\)
Khi \(W_{đ1}=0,025J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,025}{0,2}}=0,5m/s\)
Khi \(W_{đ2}=0,75J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,075}{0,2}}=0,5\sqrt 3m/s\)
Vì vận tốc biến thiên điều hoà theo thời gian, nên ta biểu diễn bằng véc tơ quay:
v O 1 0,5 0,5√3 30 0
Từ giản đồ véc tơ ta suy ra được: \(\Delta t=\dfrac{30}{360}T=\dfrac{\pi}{20}\)
\(\Rightarrow T =\dfrac{3\pi}{5}s\)
\(\Rightarrow \omega = \dfrac{2\pi}{T}=\dfrac{10}{3}\) (rad/s)
Biên độ: \(A=\dfrac{v_{max}}{\omega}=0,3m = 30cm\)

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Tổng quãng đường vật đi được trong 1 chu kì là: \(5+5+18=28cm\)
Trong 1 chu kì vật đi được quãng đường là 4A
\(\Rightarrow 4A = 28\)
\(\Rightarrow A = 7cm\)

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Khoảng thời gian vận tốc của vật không vượt quá \(6\pi cm/s\) là \(\frac{\Delta t}{T}=\frac{1}{3}\)
\(\Rightarrow\)Góc quét: \(\Delta\varphi=\frac{2\pi}{T}\frac{T}{3}=\frac{2\pi}{3}\left(rad\right)\)
\(\Rightarrow\) VTLG
-v
\(\Rightarrow\cos\varphi=\cos\left(90-30\right)=\frac{v}{v_{max}}=\frac{1}{2}\Rightarrow v_{max}=12\pi=\)\(\omega A\Rightarrow A=3,6cm\)

Đáp án D
Năng lượng của vật là: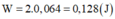
Tại t=0 thì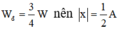
Tại t 1 thế năng bằng động năng và theo giả thiết W đ tăng đến cực đại rồi giảm, sử dụng đường tròn lượng giác ta được: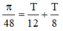 suy ra
suy ra 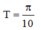 nên
nên 
Mặt khác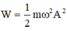 nên A=0,08(m) =8(cm)
nên A=0,08(m) =8(cm)