Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
các điểm lưới (cách đều nhau) trong hình vuông được hiển thị trong sơ đồ dưới đây, bao gồm các điểm trên các cạnh. Điểm 
nằm ở trung tâm của hình vuông. Cho rằng điểm đó 
được chọn ngẫu nhiên trong số các 
điểm khác , xác suất để đường thẳng đó 
là đường đối xứng với hình vuông là bao nhiêu?
.
.
a,Ta có:M là trung điểm AB(gt)
N là trung điểm BC(gt)
=>MN là đường trung bình tam giác ABC.
=>MN//AC và MN=1/2AC (1)
Lại có:Q là trung điểm AD(gt)
P là trung điểm DC(gt)
=>QP là đường trung bình tam giác ADC.
=>QP//AC và QP=1/2AC(2)
Từ (1)và(2)
=>MN//QP và MN=QP
=>Tứ giác MNPQ là hình bình hành.
b, <=> Góc M1 = 90°
Mà MN//AC => góc K1 = 90°
NP//MQ => góc O1 = 90°
hay AC⊥BD
Vậy tứ giác ABCD có AC⊥BD thì MNPQ là hình chữ nhật
a ) Xét \(\Delta\)ABD có :
- Q là trung điểm AD
- M là trung điểm AB
\(\Rightarrow\)QM là đường trung bình của \(\Delta\)ABD
\(\Rightarrow\)QM // BD và QM = BD / 2 ( 1 )
Xét \(\Delta\)DBC có :
- P là trung điểm DC
- N là trung điểm BC
\(\Rightarrow\)PN là\(\Rightarrow\) đường trung bình của \(\Delta\)DBC
\(\Rightarrow\)PN // BD và PN = BD / 2 ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\)◇QMCP là hình bình hành( 3 )
b ) Xét \(\Delta\)ACD có :
- Q là trung điểm AD
- P là trung điểm DC
\(\Rightarrow\)QP là đường trung bình của \(\Delta\)ACD
\(\Rightarrow\)QP // AC
Mà ta có : AC \(\perp\)BD
\(\Rightarrow\)QP \(\perp\)BD
Ta lại có :
QP \(\perp\)BD
PN // BD
\(\Rightarrow\)QP \(\perp\)PN ( 4 )
Từ ( 3 ) và ( 4 ) \(\Rightarrow\)◇QMNP là hình chữ nhật
Bài giải:
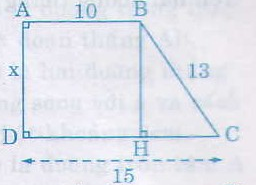
Kẻ BH ⊥ CD
Suy ra DH = 10
Nên HC = 5.
Do đó
BH2 = 132 - 52 = 169 – 25 =144
=> BH = 12
Vậy x = 12.
D
Chon D