Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Từ điểm M kẻ MH vuông góc với Ox, MK vuông góc với Oy.
Ta có: MH = 60 – 30 = 30 m.
Khi đó hoành độ điểm M là 30.
⇒ \(\;\sin \alpha {\rm{ }} = \;\frac{{MH}}{{OM}} = \;\frac{{30}}{{31}}\)
\( \Rightarrow \cos \alpha = \sqrt {1 - {{\left( {\frac{{30}}{{31}}} \right)}^2}} = \frac{{\sqrt {61} }}{{31}}\)
b, Vì các cánh quạt tạo thành 3 góc bằng nhau nên \(\widehat {MOP} = \widehat {NOP} = \widehat {MON} = {120^0}\)
\( \Rightarrow \widehat {AOP} = \widehat {MOP} - \widehat {MOA}\)
\( \Leftrightarrow \sin \widehat {AOP} = \sin \left( {\widehat {MOP} - \widehat {MOA}} \right) = \sin \widehat {MOP}.\cos \widehat {MOA} - \cos \widehat {MOP}.\sin \widehat {MOA}\)
\( = \sin \frac{{2\pi }}{3}.\cos \alpha - \cos \frac{{2\pi }}{3}.\sin \alpha \approx 0,7\)
Vì vậy chiều cao của điểm P so với mặt đất là:
31. \(\sin \widehat {AOP}\) + 60 = 31.0,7+ 60 \( \approx \) 81,76 m.
Ta có:
\(\cos \widehat {AOP} \approx \sqrt {1 - 0,{7^2}} = 0,71\)
\(\widehat {AON} = \widehat {AOP} + \widehat {PON}\)
\(\begin{array}{l} \Leftrightarrow \sin \widehat {AON} = \sin \left( {\widehat {AOP} + \widehat {PON}} \right)\\ \Leftrightarrow \sin \widehat {AON} = \sin \widehat {AOP}.\cos \widehat {PON} + \cos \widehat {AOP}.\sin \widehat {PON}\\ \Leftrightarrow \sin \widehat {AON} = 0,7.\cos \frac{{2\pi }}{3} + 0,71.\sin \frac{{2\pi }}{3} \approx 0,26\end{array}\)
\( \Rightarrow \sin \left( {OA,ON} \right) = \sin \widehat {AON} \approx 0,26\)
Vì vậy chiều cao của điểm N so với mặt đất là:
31. \(\sin \widehat {AON}\) + 60 = 31.0,26+ 60\( \approx \) 68,2 m.

Ta nhận xét rằng khi thả bóng thì bóng đi được 1 lược còn kể từ lần nảy đầu tiên đến khi dừng lại thì bóng đi được 2 lược (1 nảy lên và 1 rơi xuống). Giả sử sau lần nảy thứ n + 1 thì bóng dừng hẳn.
Quãng đường bóng đi được tính đến lần chạm sàn thứ nhất là:
\(S_1=63\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ 2 là:
\(S_2=63+63.\dfrac{1^1}{10^1}\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ (n + 1) là:
\(S_{n+1}=63+63.\left(\dfrac{1}{10}+\dfrac{1}{10^2}+...+\dfrac{1}{10^n}\right)\)
\(=63+63.\dfrac{\dfrac{1}{10}}{1-\dfrac{1}{10}}=70\left(m\right)\)
Vậy độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất là \(70\left(m\right)\)

a) Điểm G là điểm biểu diễn cho góc lượng giác có số đo \(\alpha \). Khi đó tọa độ điểm \(G\left( {3cos\alpha ;{\rm{ }}3sin\alpha } \right)\).
Chiều cao của gàu ở vị trí G đến mặt nước là: \(3{\rm{ }} + {\rm{ }}3sin\alpha \) (m).
b) Khoảng cách của gàu đến mặt nước bằng 1,5m khi \(3 + 3sin\alpha = 1,5 \Leftrightarrow sin\alpha {\rm{ }} = \frac{{ - 1}}{2}\)
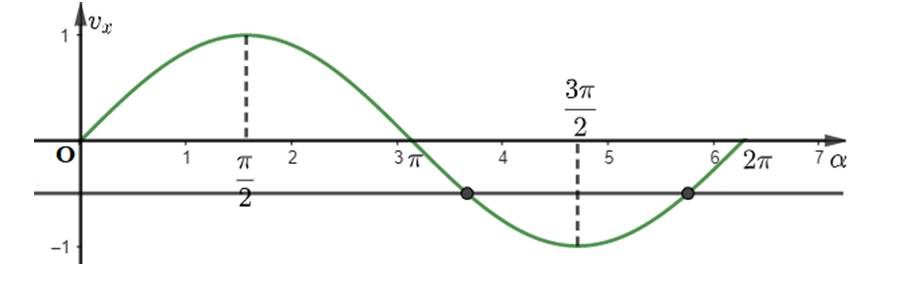
Một vòng quay là 30 giây và t nằm trong khoảng từ 0 đến 1 phút do đó t ∈ [0; 2π].

a) Hai điểm M và N đối xứng nhau qua hệ trục Oxy.
Suy ra
\(\cos ( - \alpha )\)=\(\cos \alpha \); \(\sin ( - \alpha )\)= \( - \sin \alpha \)
b) Ta có:
\(\tan ( - \alpha )\) =\( - \tan \alpha \); \(\cot ( - \alpha )\)\( - \cot \alpha \)

Ta có: \(v\left(t\right)=h'\left(t\right)=-9,8t\)
a, Vận tốc của vật tại thời điểm t = 5s là \(v\left(5\right)=-9,8\cdot5=-49\left(m/s\right)\)
b, Khi vật chạm đất thì \(h\left(t\right)=100-4,9t^2=0 \Rightarrow t=\dfrac{10\sqrt{10}}{7}\left(s\right)\)
Khi đó, vận tốc vật chạm đất là: \(v\left(\dfrac{10\sqrt{10}}{7}\right)=-9,8\cdot\dfrac{10\sqrt{10}}{7}=-14\sqrt{10}\left(m/s\right)\)

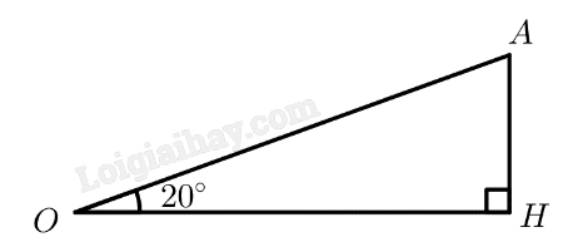
Đổi \(200km/h = \frac{{500}}{9}m/s\)
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.

Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)

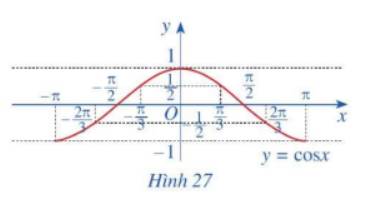
a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.