Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta có:
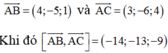
Phương trình mặt phẳng (ABC) là:
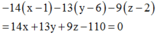
Do đó
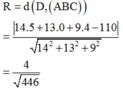
Vậy phương trình mặt cầu tâm D tiếp xúc với mặt phẳng (ABC) là:
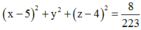

Chọn A.

+) Mặt phẳng đi qua D (4;0;6) có VTPT có phương trình:
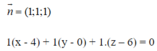
![]()

Đáp án C
Giả sử D(a;b;c).Vì ABCD là hình bình hành nên
![]()
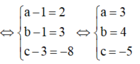
![]()
Diện tích hình bình hành ABCD là
![]()

Giải:
a) Mặt phẳng (ACD) đi qua A(5 ; 1 ; 3) và chứa giá của các vectơ (0 ; -1 ; 1)
và (-1 ; -1 ; 3).
Vectơ = (-2 ; -1 ; -1) vuông góc với mặt phẳng (ACD).
Phương trình (ACD) có dạng:
2(x - 5) + (y - 1) + (z - 3) = 0.
hay 2x + y + z - 14 = 0.
Tương tự: Mặt phẳng (BCD) qua điểm B(1 ; 6 ; 2) và nhận vectơ làm vectơ pháp tuyến.
Ta có :(4 ; -6 ; 2),
(3 ; -6 ; 4) và
= (-12 ; -10 ; -6)
Xét (6 ; 5 ; 3) thì
nên
cũng là vectơ pháp tuyến của mặt phẳng (BCD). Phương trình mặt phẳng (BCD) có dạng:
6(x - 1) + 5(y - 6) +3(z - 2) = 0
hay 6x + 5y + 3z - 42 = 0.
b) Mặt phẳng ( α ) qua cạnh AB và song song với CD thì ( α ) qua A và nhận
(-4 ; 5 ; 1) ,
(-1 ; 0 ; 2) làm vectơ chỉ phương.
Vectơ = (10 ; 9 ; 5) là vectơ pháp tuyến của ( α ).
Phương trình mặt phẳng ( α ) có dạng : 10x + 9y + 5z - 74 = 0.
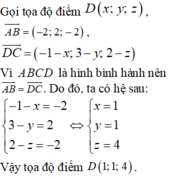
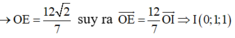
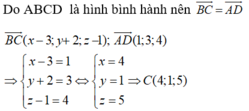
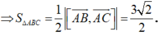
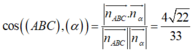
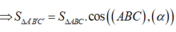
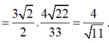
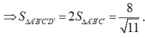
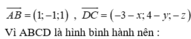
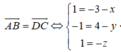

Lời giải:
Gọi tọa độ điểm \(D=(a,b,c)\). Ta có:
\(\left\{\begin{matrix} \overrightarrow{AB}=(-4,5,-1)\\ \overrightarrow{AD}=(a-5,b-1,c-3)\\ \overrightarrow {AC}=(0,-1,1)\end{matrix}\right.\)
Theo định lý về hình bình hành:
\(\overrightarrow{AB}+\overrightarrow {AD}=\overrightarrow{AC}\Leftrightarrow (a-9,b+4,c-4)=(0,-1,1)\)
\(\Rightarrow \left\{\begin{matrix} a=9\\ b=-5\\ c=5\end{matrix}\right.\)
PTMP:
Vector pháp tuyến của mặt phẳng \(\overrightarrow{n_\alpha}=[\overrightarrow{AB},\overrightarrow{AC}]=(4,4,4)\)
\(\Rightarrow \) PTMP là:: \(4(x-5)+4(y-0)+4(z-4)=0\Leftrightarrow x+y+z-9=0\)