Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

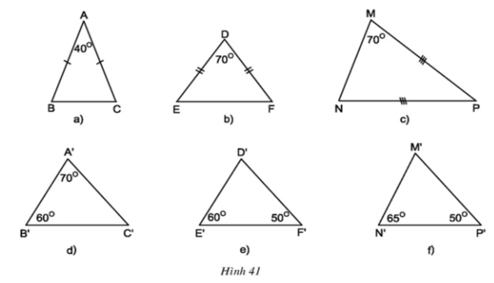
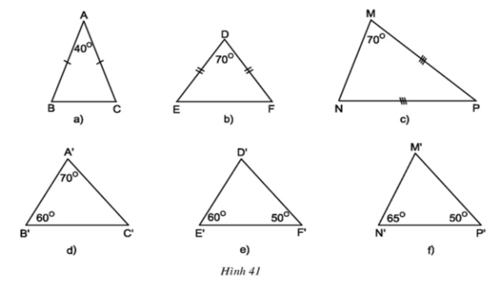
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)

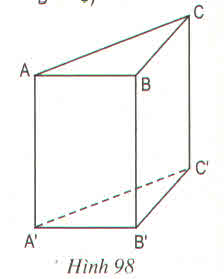
a) Những cặp mặt phẳng song song nhau: (ABC) // (A'B'C')
b) Những cặp mặt phẳng vuông góc với nhau: (ABB'A') ⊥ (A'B'C); (ACC'A') ⊥ (A'B'C'); (BCC'B') ⊥ (A'B'C); (ABB'A') ⊥ (ABC); (ACC'A') ⊥ (ABC); (BCC'B') ⊥ (ABC)
c) Điền vào ô trống:

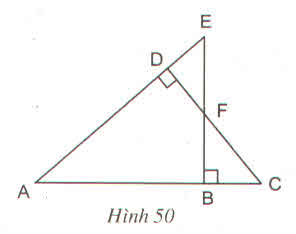
∆ADC ∽ ∆ABE vì góc A chung và \(\widehat{D}\)= \(\widehat{B}\) = 900
∆DEF ∆BCF vì \(\widehat{D}\) = \(\widehat{B}\) = 900 , \(\widehat{DEF}=\widehat{BFC}\)
∆DFE ∆BAE vì ( \(\widehat{D}=\widehat{B}\) = 900 , góc A chung)
∆BFC ∆DAC vì (\(\widehat{D}=\widehat{B}\) = 900, góc C chung)


A B C K H I
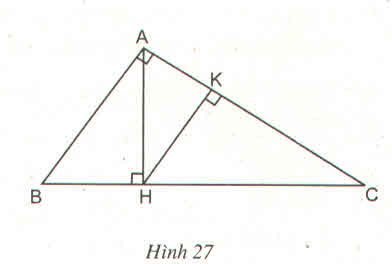
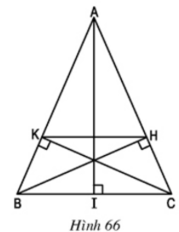
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)












- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)