Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các khẳng định đúng là: (1) ; (2); (3)
(4) cần sửa thành: Phương sai là bình phương của độ lệch chuẩn.
Chọn C

a)
+) Tỉnh Lai Châu: Xét mẫu số liệu đã sắp xếp là:
\(\begin{array}{*{20}{c}}{14,2}&{14,8}&{18,6}&{18,8}&{20,3}&{21,0}&{22,7}&{23,5}&{23,6}&{24,2}&{24,6}&{24,7}\end{array}\)
Khoảng biến thiên của mẫu số liệu là: \(R = 24,7 - 14,2 = 10,5.\)
Cỡ mẫu là \(n = 12\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 21,85.\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(\begin{array}{*{20}{c}}{14,2}&{14,8}&{18,6}&{18,8}&{20,3}&{21,0}\end{array}\). Do đó \({Q_1} = 18,7.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(\begin{array}{*{20}{c}}{22,7}&{23,5}&{23,6}&{24,2}&{24,6}&{24,7}\end{array}\). Do đó \({Q_3} = 23,9\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 23,9 - 18,7 = 5,2\)
+) Tỉnh Lâm Đổng: Xét mẫu số liệu đã sắp xếp là:
\(16,0\;\;16,3\;\;17,4\;\;17,5\;\;18,5\;\;18,6\;\;18,7\;\;19,3\;\;19,5\;\;19,8\;\;20,2\;\;20,3\)
Khoảng biến thiên của mẫu số liệu là: \(R = 20,3 - 16,0 = 4,3.\)
Cỡ mẫu là \(n = 12\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 18,65.\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(\begin{array}{*{20}{c}}{16,0}&{16,3}&{17,4}&{17,5}&{18,5}&{18,6}\end{array}\). Do đó \({Q_1} = 17,45.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(\begin{array}{*{20}{c}}{18,7}&{19,3}&{19,5}&{19,8}&{20,2}&{20,3}\end{array}\). Do đó \({Q_3} = 19,65\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 19,65 - 17,45 = 2,2\)

Chọn C.
Ta có bảng phân bố tần suất
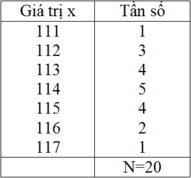
Do giá trị 114 có tần số lớn nhất là 5 nên ta có: M0 = 114.

• Ta có:
- Số trung bình cộng x = 55,82 trường là không có nghĩa.
- Trong các số liệu thống kê đã cho có sự chênh lệch quá lớn (điều này chứng tỏ các số liệu thống kê đã cho là không cùng loại)
Chỉ cần một trong hai điều kể trên là đủ để suy ra rằng: Không chọn được số trung bình cộng làm đại diện cho các số liệu thống kê.
• Dễ thấy: Bảng số liệu thống kê đã cho không có mốt.
• Trong trường hợp đã cho, ta chọn số trung vị M e = 40 (trường) để làm đại diện cho các số liệu thống kê đã cho (về quy mô và độ lớn).
Đáp án: B

Bảng phân bố tần số- tần suất:
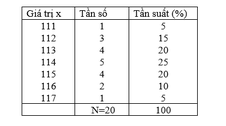
Số trung bình:
x - = 1 20 ( 1 . 111 + 3 . 112 + 4 . 113 + 5 . 114 + 4 . 115 + 2 . 116 + 1 . 117 ) = 113 , 9
Chọn D

a) Bảng phân bố tần số:
| Tuổi thọ | Tần số |
| 1150 | 3 |
| 1160 | 6 |
| 1170 | 12 |
| 1180 | 6 |
| 1190 | 3 |
| Cộng | 30 |
Bảng phân bố tần suất:
| Tuổi thọ | Tần suất |
| 1150 | 10% |
| 1160 | 20% |
| 1170 | 40% |
| 1180 | 20% |
| 1190 | 10% |
| Cộng | 100% |
b) Nhận xét: phần lớn các bóng đèn có tuổi thọ từ 1160 đến 1180 giờ.

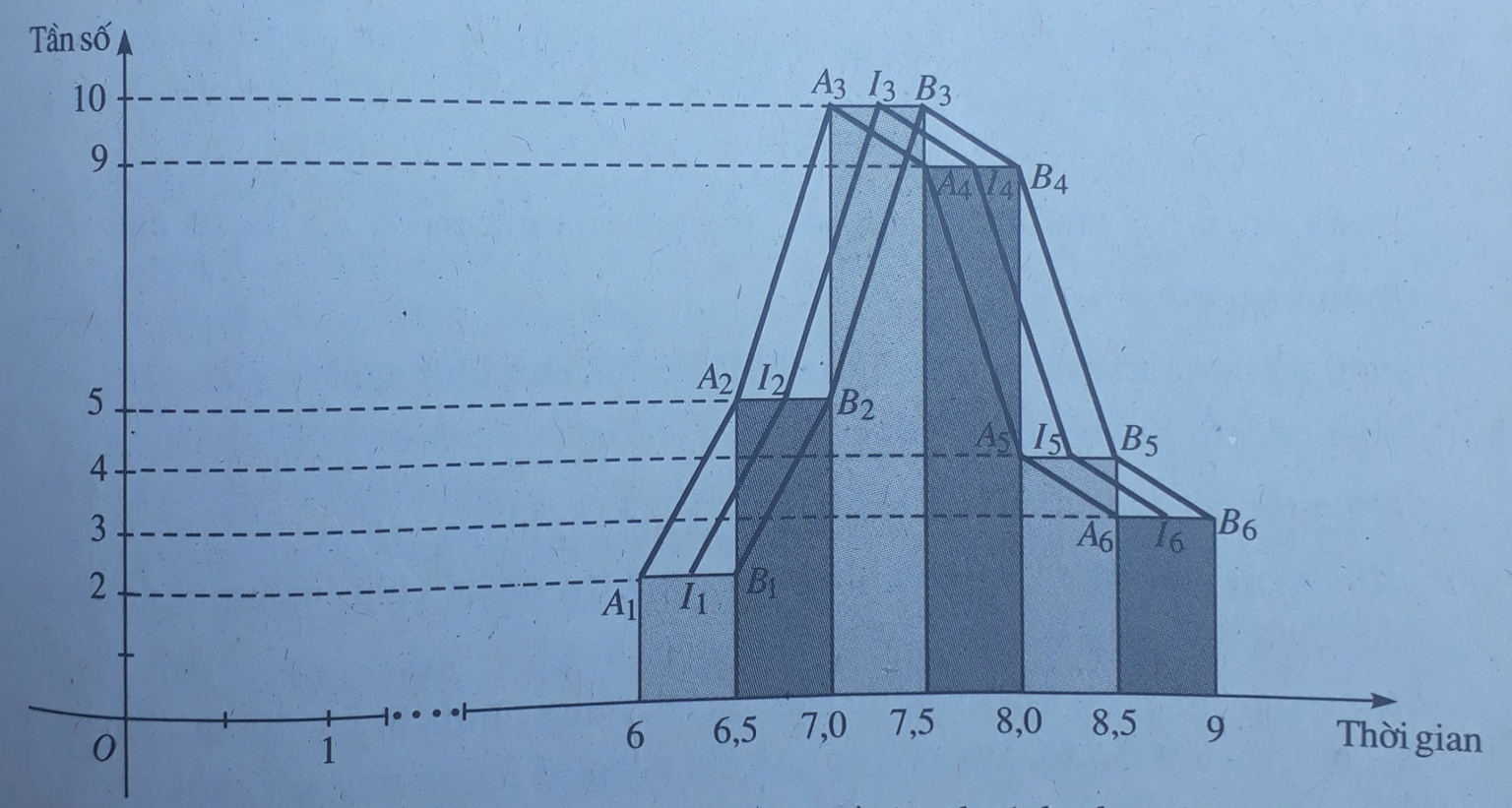
Các đỉnh của đường gấp khúc tần số có tọa độ là ( c i ; n i ), với c i là giá trị đại diện của lớp thứ i, n i là tần số của lớp thứ i. Từ đó suy ra: các đỉnh của đường gấp khúc tần số là các trung điểm của các cạnh phía trên của các cột (các hình chữ nhật) của biểu đồ tần số hình cột
Đường gấp khúc I 1 I 2 I 3 I 4 I 5 I 6 với I 1 , I 2 , I 3 , I 4 , I 5 , I 6 lần lượt là trung điểm của các đoạn thẳng A 1 B 1 , A 2 B 2 , A 3 B 3 , A 4 B 4 , A 5 B 5 , A 6 B 6

a) Số trung bình \(\overline{x}=6,6\) triệu đồng. Số trung vị \(M_e=6\) triệu đồng. Mốt \(M_0=6\) triệu đồng
b) Trong các số liệu thống kê đã cho có sự chênh lệch nhau quá lớn, nên ta không chọn số trung bình cộng mà chọn số trung vị \(M_e=6\) triệu đồng, làm đại diện cho mức thu nhập trong năm 2000 của mỗi gia đình trong 31 gia đình được khảo sát.





Thống kê là khoa học nghiên cứu các phương pháp thu thập; phân tích và xử lí các số liệu
chọn D