
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


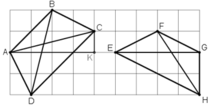
+ Xét tứ giác ABCD
Nhận thấy AB // CD ⇒ Tứ giác ABCD là hình thang.
Xét ΔACK vuông tại K ta có: AC2 = AK2 + KC2 = 42 + 12 = 17
Tương tự ta có BD2 = 42 + 12 = 17
⇒ AC2 = BD2
⇒ AC = BD
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
+ Xét tứ giác EFGH
FG // EH ⇒ Tứ giác EFGH là hình thang.
Lại có : EG = 4cm
FH2 = 22 + 32 = 13 ⇒ FH = √13 ≠ EG.
Vậy hình thang EFGH có hai đường chéo không bằng nhau nên không phải hình thang cân.

Lời giải:
a. $BAC$ là tam giác vuông cân tại $A$
$\Rightarrow \widehat{BCA}=45^0$
$ACE$ là tam giác vuông cân tại $E$
$\Rightarrow \widehat{EAC}=45^0$
Do đó: $\widehat{BCA}=\widehat{EAC}$. Mà 2 góc này ở vị trí so le trong nên $AE\parallel BC$. Mà $\widehat{E}=90^0$ nên $AECB$ là hình thang vuông.
-----------------
Tính góc:
Hình thang vuông $AECB$ có $\widehat{E}=90^0$ đương nhiên $\widehat{C}=180^0-\widehat{E}=90^0$
$\widehat{ABC}=45^0$ (do $ABC$ vuông cân tại $A$)
$\widehat{BAE}=\widehhat{BAC}+\widehat{EAC}=90^0+45^0=135^0$
Tính cạnh:
Vì $ABC$ vuông cân tại $A$ nên $AB=AC$
Áp dụng định lý Pitago:
$AB^2+AC^2=BC^2=4$
$AB^2+AB^2=4$
$2AB^2=4\Rightarrow AB=\sqrt{2}$ (cm)
$\Rightarrow AC=\sqrt{2}$ (cm)
Áp dụng định lý Pitago cho tam giác $ACE$ vuông cân tại $E$:
$AE^2+EC^2=AC^2=2$
$2AE^2=2\Rightarrow AE=1$ (cm)
$EC=AE=1$ (cm)
Vậy.........

Câu 3.
Tam giác \(ABC\)vuông cân tại \(A\)nên \(\widehat{ACB}=45^o\).
Tam giác \(BCD\)vuông cân tại \(B\)nên \(\widehat{BCD}=45^o\).
\(\widehat{ACD}=\widehat{ACB}+\widehat{BCD}=45^o+45^o=90^o\)
\(\Rightarrow AC\perp CD\)
mà \(AC\perp AB\)
nên \(AB//CD\)
suy ra \(ABCD\)là hình thang vuông.
Câu 4.
Kẻ \(BE\perp CD\)khi đó \(\widehat{BED}=90^o\).
Tứ giác \(ABED\)có \(4\)góc vuông nên là hình chữ nhật, mà \(AB=AD\)nên \(ABED\)là hình vuông.
\(BE=DE=AB=2\left(cm\right)\)
\(EC=CD-DE=4-2=2\left(cm\right)\)
Suy ra tam giác \(BEC\)vuông cân tại \(E\)
Suy ra \(\widehat{EBC}=\widehat{ECB}=45^o\)
\(\widehat{ABC}=\widehat{ABE}+\widehat{EBC}=90^o+45^o=135^o\)

Tam giác BCD có :
BN = NC ( gt )
DP = PC ( gt )
\(\Rightarrow\)NP là đường trung bình tam giác BCD ( 1 )
Tam giác ADB có :
AQ = QD ( gt )
AM = MB ( gt )
\(\Rightarrow\)QM là đường trung bình tam giác ADB ( 2 )
Từ ( 1 ) , ( 2 ) suy ra NP = QM , NP // QM
\(\Rightarrow\)MNEF là hình bình hành ( đến đây bạn tự chứng minh tiếp hình thoi )
c) Để MNPQ là hình vuông thì ta chứng minh ABCD là hình thang cân có 2 đường chéo vuông góc với nhau

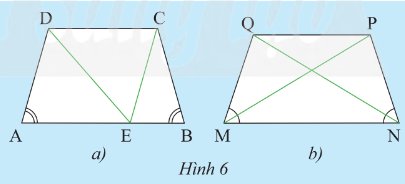
a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)

a: Xét ΔABC có
\(\dfrac{CM}{MN}=\dfrac{CA}{AB}\)
Do đó: MN//AB
hay MN\(\perp\)AC
Xét ΔCMN cân tại M có \(\widehat{CMN}=90^0\)
nên ΔCMN vuông cân tại M
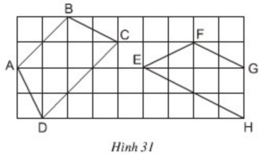
hình 1,2,3 là hình thang cân
hình 1: ab//dc ; ab = ac
hình 2: góc h = góc g
hình 3: LI=JR