Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

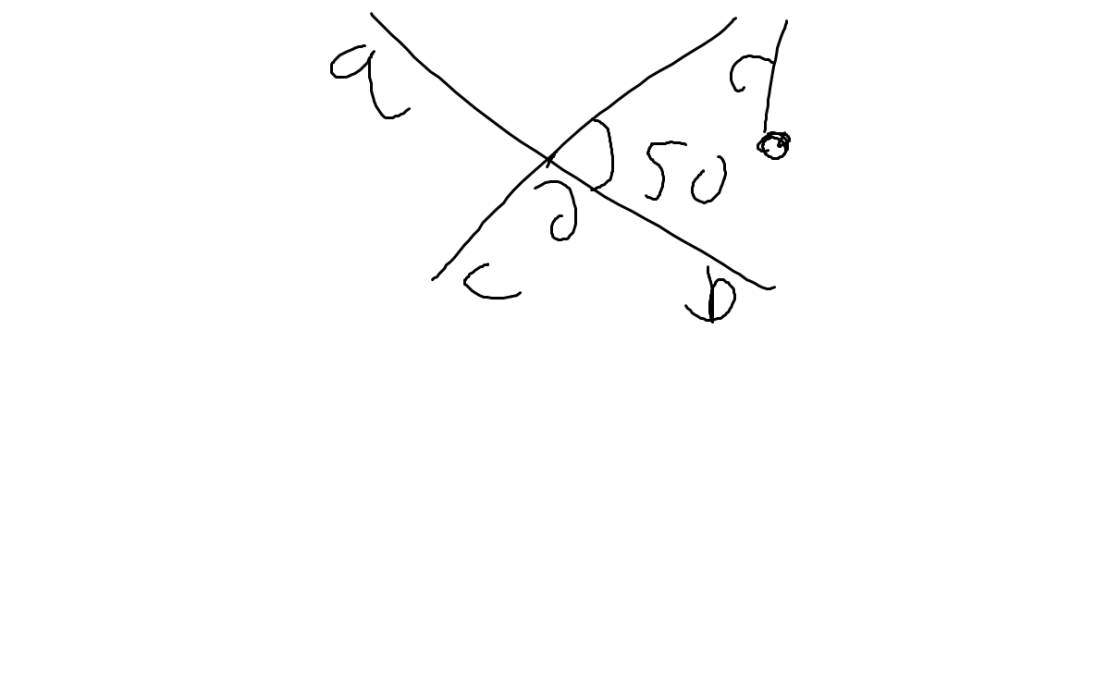
Gọi hai đường thẳng đề bài cho là ab và cd. Gọi O là giao của ab và cd
a: góc bOd và góc aOc
góc aOd và góc bOc
b: góc aOc=góc bOd=50 độ
góc aOd=góc bOc=180-50=130 độ

Gọi hai đường thẳng cắt nhau là xx' và yy'. Gọi điểm cắt giữa hai đường thẳng là O
a/ Các cặp góc đối đỉnh là: góc xOy đối đỉnh với góc y'Ox' ; góc x'Oy đối đỉnh với góc xOy'
b/ Gọi góc xOy = 50o
Vì góc xOy đối đỉnh với góc y'Ox'
suy ra góc xOy = y'Ox' = 50o
Vì hai đường thẳng xx' và yy' cắt nhau tại O
Suy ra tia Ox và tia Ox' đối nhau ; tia Oy và tia Oy' là hai tia đối nhau
Suy ra góc xOy và góc yOx' kề bù
Suy ra góc xOy + góc yOx' = 180o
50o + góc yOx' = 180o ( vì góc xOy = 50o )
góc yOx' = 180o - 50o = 130o
Vì góc yOx' và góc xOy' là hai góc đối đỉnh
Suy ra góc yOx' = góc xOy' = 130o
Vậy: ........... ( bạn tự viết nhé )
Nhớ k cho mình nhé! Thank you!!!

Nếu có 3 đường thẳng cắt nhau tại 1 điểm thì chúng tạo thành 6 tia chung gốc.
Mỗi tia tạo với 5 tia còn lại 5 góc mà có 6 tia như vậy nên có tất cả số góc là:
5 x 6 = 30 góc
Vì mỗi góc được tính lặp lại 2 lần nên có tất cả:
30 : 2 = 15 góc
3 đường thẳng cắt nhau tạo thành 3 góc bẹt. Vậy có tất cả số góc khác góc bẹt là:
15 - 3 = 12 góc khác góc bẹt
Có tất cả 12 góc khác góc bẹt mà mỗi góc có 1 góc đối đỉnh với nó. Nên có tất cả:
12 : 2 = 6 cặp góc đối đỉnh
Nguồn: https://h.vn/hoi-dap/question/87465.html
b,https://olm.vn/hoi-dap/question/181733.html
bạn click vô link sẽ dẫn đến bài viết

M N P Q O 60 t t'
a)vì mop và Qon đối dỉnh => \(\widehat{mop}=\widehat{qon}=60^o\)
vì mn là đường thẳng => \(\widehat{mon=180}\)
có \(180^o>60^o\Rightarrow\widehat{mon}>\widehat{mop}\)
vậy tia op nawmf giữa hai tia om và on
vậy \(\widehat{mop}+\widehat{pon}=\widehat{mon}\)
thay\(60^o+\widehat{pon}=180^o\)
\(\Leftrightarrow\widehat{pon}=180-60=120\)
vì pon và moq đối đỉnh =>pon=moq=120
b) là qot' và top ; t'on và mot;mop và qon
M N P Q t t'
Giải :
a) Ta có: \(\widehat{MOP}+\widehat{PON}=180^0\)(kề bù)
=> \(\widehat{PON}=180^0-\widehat{MOP}=180^0-60^0=120^0\)
Ta lại có:
+) \(\widehat{MOP}=\widehat{QON}\) (đối đỉnh)
mà \(\widehat{MOP}=60^0\) => \(\widehat{QON}=60^0\)
+) \(\widehat{NOP}=\widehat{MOQ}\) (đối đỉnh)
Mà \(\widehat{NOP}=120^0\) => \(\widehat{MOQ}=120^0\)
b) Các cặp góc đối đỉnh là góc nhọn
+) \(\widehat{MOP}\) và \(\widehat{NOQ}\)
+) \(\widehat{MOQ}\) và \(\widehat{NOP}\)
+) \(\widehat{MOt}\) và \(\widehat{NOt'}\)
+) \(\widehat{tOP}\) và \(\widehat{t'OQ}\)
+) \(\widehat{QOt}\) và \(\widehat{POt'}\)
+) ...
Tự liệt kê
Góc nhọn
Góc vuông
Góc tù
Góc bẹt