Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hai tam giác vuông DAC và DBA ,ta có:
∠ (ADC) = ∠ (BDA) = 90 0
∠ C = ∠ (DAB) (hai góc cùng phụ ∠ B )
Suy ra: △ DAC đồng dạng △ DBA (g.g)
Suy ra: 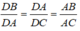
⇒ D A 2 = D B . D C
hay DA = D B . D C = 9 . 16 = 12 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
A B 2 = D A 2 + D B 2 = 9 2 + 12 2 = 225 ⇒ AB =15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:
AC2 = DA2 + DC2 = 122 +162 = 400 ⇒ AC = 20cm
Vậy BC = BD + DC = 9 + 16 = 25(cm)

A B C D E 6 H
a) BC = \(\sqrt{AB^2+AC^2}\)= \(\sqrt{6^2+8^2}\)= \(\sqrt{100}\)= 10 (theo định lí Pythagoras)
\(\Delta\)ABC có BD là phân giác => \(\frac{AD}{AB}\)= \(\frac{CD}{BC}\)= \(\frac{AD}{DC}\)= \(\frac{AB}{BC}\)= \(\frac{6}{10}\)= \(\frac{3}{5}\).
b) Ta có : \(\widehat{ABE}\)= \(\widehat{EBC}\)(BD là phân giác)
=> \(\Delta ABD\)~ \(\Delta EBC\)(gg)
=> \(\frac{BD}{BC}\)= \(\frac{AD}{EC}\)<=> BD.EC = AD.BC (đpcm).
c) Ta có : \(\Delta CHE\)~ \(\Delta CEB\)( 2 tam giác vuông có chung góc C )
=> \(\frac{CH}{CE}\)= \(\frac{CE}{CB}\)<=> CH.CB = CE2 (1)
\(\Delta CDE\)~ \(\Delta BDA\)(gg (2 góc đối đỉnh))
\(\Delta BDA~\Delta BCE\) (câu b))
=> \(\Delta CDE~\Delta BCE\)
=> \(\frac{CE}{BE}\)= \(\frac{DE}{CE}\)<=> BE.DE = CE2 (2)
Từ (1) và (2) => CH.CB = ED.EB (đpcm).

Thầy ơi,các bạn ơi giúp mình với, 2 ngày nữa là han nộp rồi.

Gọi tam giác vuông cân đó là ABC
Ta có:\(\frac{AB+AC}{2}=\sqrt{2}\Leftrightarrow\frac{2AC}{2}=\sqrt{2}.\)
\(\Rightarrow AB=AC=\sqrt{2}\)

A C B H D M K
Qua B kker đường thẳng song song với AC cắt AD tại H
=> BH vuông AB
Xét tam giác ABH và tam giác CAM
Có \(\widehat{ABH}=\widehat{CAM}=90^o\)
AB =AC ( ytam giác ABC cân)
\(\widehat{BAH}=\widehat{ACM}\)( cùng phụ với góc AMC)
=> Tam giác ABH=CAM
=> BH=MA
Vì BH//AC theo định lí thales
\(\frac{BD}{DC}=\frac{BH}{AC}=\frac{AM}{AB}=\frac{1}{2}\)
A B C M H
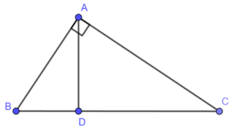
Tam giác ABC vuông tại A với đường cao AH và trung tuyến AM
Theo tính chất trung tuyến ứng với cạnh huyền, ta có \(AM=\dfrac{BC}{2}\)
\(\dfrac{AH}{AM}=\dfrac{40}{41}\Leftrightarrow\dfrac{AH}{\dfrac{BC}{2}}=\dfrac{40}{41}\Leftrightarrow AH=\dfrac{20}{41}BC\) (1)
Xét hai tam giác vuông ABH và CBA có \(\widehat{B}\) chung
\(\Rightarrow\Delta ABH\sim\Delta CBA\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{BC}\Leftrightarrow AB.AC=AH.BC\) (2)
Thay (1) vào (2): \(AB.AC=\dfrac{20}{41}BC^2\Leftrightarrow\dfrac{41}{20}AB.AC=BC^2\)
Theo định lý Pitago: \(AB^2+AC^2=BC^2\Rightarrow AB^2+AC^2=\dfrac{41}{20}AB.AC\) (3)
Do các cạnh tam giác đều lớn hơn 0, chia 2 vế của (3) cho \(AB.AC\):
\(\dfrac{AB}{AC}+\dfrac{AC}{AB}=\dfrac{41}{20}\Rightarrow\) đặt \(\dfrac{AB}{AC}=x>0\) ta được:
\(x+\dfrac{1}{x}=\dfrac{41}{20}\Leftrightarrow x^2-\dfrac{41}{20}x+1=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{4}{5}\end{matrix}\right.\)
Vậy tỉ số giữa 2 cạnh góc vuông là \(\dfrac{4}{5}\) ( hoặc \(\dfrac{5}{4}\))