Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE và \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó: ΔDBF=ΔDEC

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)

Hình vẽ, giả thiết, kết luận bạn vẽ và làm nha
\(a,\Delta DAB=\Delta DEC\)
\(\text{Xét }\Delta DAB=\Delta DEC\text{ có: }\)
\(DA=DE\left(gt\right)\left(1\right)\)
\(\widehat{ADB}=\widehat{EDC}\left(\text{đối đỉnh}\right)\left(2\right)\)
\(BD=CD\left(gt\right)\left(3\right)\)
\(\text{Từ (1), (2) và (3)}\Rightarrow\Delta DAB=\Delta DEC\left(c.g.c\right)\left(đpcm\right)\)
\(b,AC\text{//}BE\)
\(\text{Xét }\Delta ADC=\Delta EDB\text{ có: }\)
\(DA=DE\left(gt\right)\left(4\right)\)
\(\widehat{ADC}=\widehat{EDB}\left(\text{đối đỉnh}\right)\left(5\right)\)
\(CD=BD\left(gt\right)\left(6\right)\)
\(\text{Từ (4), (5) và (6)}\Rightarrow\Delta ADC=\Delta EDB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DAC}=\widehat{DEB}\left(\text{2 góc tương ứng}\right)\)
\(\text{Mà 2 góc này ở vị trí so le trong của 2 đoạn thẳng AC và BE}\)
\(\Rightarrow AC\text{//}BE\left(đpcm\right)\)
\(c,F,D,G\text{ thẳng hàng}\)
\(\text{Ta có: }\Delta DAB=\Delta DEC\left(\text{câu a}\right)\)
\(\Rightarrow\widehat{BAD}=\widehat{CED}\left(\text{2 góc tương ứng}\right)\)
\(\text{Hay }\widehat{FAD}=\widehat{GED}\)
\(\text{Xét }\Delta ADF=\Delta EDG\text{ có: }\)
\(DA=DE\left(gt\right)\left(7\right)\)
\(\widehat{FAD}=\widehat{GED}\left(cmt\right)\left(8\right)\)
\(AF=EG\left(gt\right)\left(9\right)\)
\(\text{Từ (7), (8) và (9)}\Rightarrow\Delta ADF=\Delta EDG\left(c.g.c\right)\)
\(\Rightarrow\widehat{ADF}=\widehat{EDG}\left(\text{2 góc tương ứng}\right)\)
\(\text{Lại có:}\widehat{EDG}+\widehat{ADG}=180^o\left(\text{kề bù}\right)\)
\(\text{Mà }\widehat{EDG}=\widehat{ADF}\left(cmt\right)\)
\(\Rightarrow\widehat{ADF}+\widehat{ADC}=180^o\left(10\right)\)
\(AD\text{ chung}\left(11\right)\)
\(\text{F và G khác phía đối với D}\left(12\right)\)
\(\text{Từ (10), (11) và (12)}\Rightarrow F,D,G\text{ thẳng hàng}\)
\(\text{Lưu ý: Bạn không thể chứng minh }\widehat{ADF}=\widehat{EDG}\text{ vì 2 góc đối đỉnh},\text{do nếu chứng}\)
\(\text{minh như vậy thì nghiễm nhiên bạn đã công nhân F,D,G thẳng hàng }\)
phần c bạn ko cần lm dài vậy đâu.Bạn chỉ cần xét tam giác AFD và tam giác EDG rùi suy ra 2 cnh FD=DG mà 3 điểm B,D,C thẳng hàng=>3 điểm F,D,G thẳng hàng là xong.Chứ bạn cm vậy đúng nhx dài dòng quá.Đây là ý kiến của mình ,nếu bn muốn bạn vẫn có thể lm theo cách của bạn kia đã lm ở trên

a: Xét ΔADF và ΔADC có
AD chung
\(\widehat{FAD}=\widehat{CAD}\)
AF=AC
Do đó: ΔADF=ΔADC
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE và \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{FBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{FBD}=\widehat{CED}\)
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó: ΔDBF=ΔDEC
=>\(\widehat{BDF}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{BDE}=180^0\)(hai góc kề bù)
nên \(\widehat{BDE}+\widehat{BDF}=180^0\)
=>E,D,F thẳng hàng
c: Ta có: ΔDBF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của CF(1)
ta có: AF=AC
=>A nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra AD là đường trung trực của CF
=>AD\(\perp\)CF

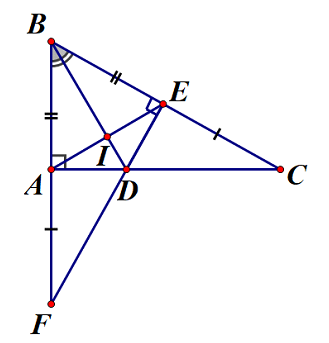
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>DA=DE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>E,D,F thẳng hàng

Đề thiếu rồi bạn