Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có 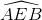 là góc có đỉnh ở bên ngoài đường tròn nên:
là góc có đỉnh ở bên ngoài đường tròn nên:
\(\widehat{AEB}=\dfrac{sđ\left(\widehat{AB}-\widehat{CD}\right)}{2}=\dfrac{180^O-60^O}{2}=60^O\)
và \(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:
\(\widehat{BTC}\) = sđ\(\dfrac{\widehat{BAC}-\widehat{BDC}}{2}=\dfrac{\left(180^O+60^O\right)-\left(60^O+60^O\right)}{2}=60^O\)
Vậy 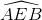 =
=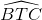
b) \(\widehat{DCT}\) là góc tạo bởi tiếp tuyến và dây cung nên:
\(\widehat{DCT}=\dfrac{sđ\widehat{CD}}{2}=\dfrac{60^o}{2}=30^o\)
→ \(\widehat{DCB}\) là góc nội tiếp trên
\(\widehat{DCB}\) = \(\dfrac{sđ\widehat{DB}}{2}\) = \(\dfrac{60^O}{2}=30^O\)
Vậy \(\widehat{DCT}\) = \(\widehat{DCB}\) hay CD là phân giác của \(\widehat{BCT}\)

a. Xét \(\Delta OAB:\)\(AB^2=2R^2\)
\(OA^2+OB^2=R^2+R^2=2R^2\)
Vậy \(\Delta OAB\) vuông tại O.
\(\Rightarrow l_{\stackrel\frown{AB}}=\frac{\pi R.90}{180}=\frac{1}{2}\pi R\)
Có: \(l_{\stackrel\frown{BC}}=l_{\stackrel\frown{AC}}-l_{\stackrel\frown{AB}}\)\(=\frac{\pi R.120}{180}-\frac{1}{2}\pi R\)\(=\frac{1}{6}\pi R\)
c.Ace Legona, Nguyễn Việt Lâm tính giùm mk.
O A C H
\(\widehat{AOC}=120^0\Rightarrow\widehat{AOH}=60^0\)
\(\Rightarrow AH=OA.sin\widehat{AOH}=R.sin60^0=\frac{R\sqrt{3}}{2}\)
\(\Rightarrow AC=2AH=R\sqrt{3}\)
O B C P
\(\widehat{BOC}=\widehat{AOC}-\widehat{AOB}=30^0\)
Kẻ \(CP\perp OB\Rightarrow\left\{{}\begin{matrix}CP=OC.sin\widehat{POC}=R.sin30^0=\frac{R}{2}\\OP=OC.cos\widehat{POC}=R.cos30^0=\frac{R\sqrt{3}}{2}\end{matrix}\right.\)
\(BP=OB-OP=R-\frac{R\sqrt{3}}{2}=\frac{R\left(2-\sqrt{3}\right)}{2}\)
Áp dụng Pitago cho tam giác BCP:
\(BC=\sqrt{BP^2+CP^2}=R\sqrt{2-\sqrt{3}}\)
 giúp mk
giúp mk