Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
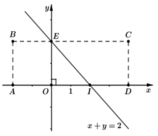
Để con châu chấu đáp xuống các điểm M(x; y) có x + y < 2 thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x; y) có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 , y ∈ { 0 ; 1 ; 2 }
Nếu x ∈ - 2 ; - 1 thì y ∈ { 0 ; 1 ; 2 } có 2.3 = 6 điểm
Nếu x = 0 thì y ∈ { 0 ; 1 } có 2 điểm
Nếu x =1 => y = 0 => có 1 điểm
=> có tất cả 6 + 2 + 1 = 9 điểm. Để con châu chấu nhảy trong hình chữ nhật mà đáp xuống các điểm có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 , y ∈ { 0 ; 1 ; 2 } . Số các điểm M(x; y) có tọa độ nguyên là: 7.3 = 21 điểm. Xác suất cần tìm là: P = 9 21 = 3 7 .

a) Gọi M' (x₁' ; y₁' ), N' (x₂' ; y₂ )
* M' là ảnh của M qua phép F, nên toạ độ M' thoả:
{x₁' = x₁.cosα – y₁.sinα + a
{y₁' = x₁.sinα + y₁.cosα + b
* N' là ảnh của N qua phép F, nên toạ độ N' thoả:
{x₂' = x₂.cosα – y₂.sinα + a
{y₂' = x₂.sinα + y₂.cosα + b
b) * Khoảng cách d giữa M và N là:
d = MN = √ [(x₂ - x₁)² + (y₂ - y₁)²]
* Khoảng cách d' giữa M' và N' là:
d' = M'N' = √ [(x₂' - x₁' )² + (y₂' - y₁' )²]
= √ {[x₂.cosα – y₂.sinα + a - (x₁.cosα – y₁.sinα + a)]² + [x₂.sinα + y₂.cosα + b - (x₁.sinα + y₁.cosα + b)]²}
= √ {[cosα(x₂ - x₁) - sinα(y₂ - y₁)]² + [sinα(x₂ - x₁) + cosα(y₂ - y₁)]²}
= √ [(x₂ - x₁)².(cos²α + sin²α) + (y₂ - y₁)².(cos²α + sin²α)]
= √ [(x₂ - x₁)² + (y₂ - y₁)²]
c) Phép F là phép dời hình vì: MN = M'N' = √ [(x₂ - x₁)² + (y₂ - y₁)²]
d) Khi α = 0 ⇒ cosα = 1, sinα = 0
Suy ra:
{x' = x + a
{y' = y + b
Đây là biểu thức toạ độ của phép tịnh tiến. Vậy F là phép tịnh tiến



Chọn C
Lời giải. Số các điểm có tọa độ nguyên thuộc hình chữ nhật là 7.3 = 21 điểm vì
Để con châu chấu đáp xuống các điểm M(x,y) có x + y < 2
thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x,y) có tọa độ nguyên thì
= Nếu x ∈ - 2 ; - 1 thì y ∈ 0 ; 1 ; 2
⇒ có 6 điểm
= Nếu x = 0 thì y ∈ 0 ; 1 ⇒ có 2 điểm
= Nếu x = 1 ⇒ y = 0 ⇒ có 1 điểm
⇒ có tất cả 6 + 2 +1 = 9 điểm thỏa mãn
Vậy xác suất cần tính P = 9 21 = 3 7