Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C H
Vẽ hơi xấu
Tam giác AHC vuông tại H
Áp dụng định lí py-ta-go ta có :
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=\sqrt{400}=20\left(cm\right)\)
Tam giác AHB vuông tại H
Áp dụng định lí py-ta-go ta có :
\(BH=\sqrt{AB^2-AH^2}=\sqrt{13^2-12^2}=\sqrt{25}=5\left(cm\right)\)
\(\Rightarrow BC=BH+HC=5+16=21\left(cm\right)\)

A B C D E G F H M N
ta có góc DAC = góc EAB = 90 độ (gt)
suy ra \(\widehat{DAB}+\widehat{BAC}=\widehat{EAC}+\widehat{BAC}\) (vì tia AB nằm giữa 2 tia AD và AC , tia AC nằm giữa 2 tia AE và AB )
hay \(\widehat{DAC}=\widehat{EAB}\)
\(\Delta DAC\)và\(\Delta BAE\)có \(\hept{\begin{cases}AD=AB\left(gt\right)\\\widehat{DAC}=\widehat{EAB}\left(cmt\right)\\AE=AC\left(gt\right)\end{cases}}\)
do đó \(\Delta DAC=\Delta BAE\left(c.g.c\right)\)
suy ra \(DC=BE\)(2 góc tương ứng)
và \(\widehat{EBA}=\widehat{CDA}\)( 2 góc tương ứng )
gọi giao điểm của AB và CD là G , giao điểm của DC và BE là F
\(\Delta ADG\)và \(\Delta GBF\)có \(\hept{\begin{cases}\widehat{D}=\widehat{B}\left(cmt\right)\\\widehat{DGA}=\widehat{BGF}\\\Rightarrow\widehat{BFG}=\widehat{DAG}=90^o\end{cases}}\)(đối đỉnh)
hay \(BE⊥DC\)
b) ta có góc DAH là góc ngoài của tam giác AMD
suy ra \(\widehat{DAH}=\widehat{AMD}+\widehat{ADM}\) hay \(\widehat{DAB}+\widehat{BAH}=\widehat{AMD}+\widehat{ADM}\)(vì tia AB nằm giữa 2 tia AD và AH )
mà \(\widehat{DAB}=\widehat{AMD}=90^o\)\(\Rightarrow\widehat{BAH}=\widehat{ADM}\)
\(\Delta ABH\)và\(\Delta DAM\)có \(\hept{\begin{cases}DA=BA\left(gt\right)\\\widehat{BAH}=\widehat{ADM}\left(cmt\right)\end{cases}}\)
do đó \(\Delta ABH=\Delta DAM\)(cạnh huyền - góc nhọn )
suy ra AH =DM ( 2 cạnh tương ứng )
theo đề và từ hình vẽ ta có MN trùng AH
ta có góc EAH là góc ngoài của tam giác ANE
\(\Rightarrow\widehat{EAH}=\widehat{ANE}+\widehat{AEN} hay \widehat{EAC}+\widehat{HAC}=\widehat{ANE}+\widehat{AEN}\)
mà \(\widehat{EAC}=\widehat{ANE}=90^o\)\(\Rightarrow\widehat{HAC}=\widehat{AEN}\)
\(\Delta ACH\)và\(\Delta EAN\)có
cạnh huyền AC = cạnh huyền AE
\(\widehat{HAC}=\widehat{AEN}\left(cmt\right)\)
do đó \(\Delta ACH=\Delta EAN\)(cạnh huyền góc nhọn )
suy ra AH = NE ( 2 cạnh tương ứng )
mà AH =DM
suy ra DM = NE
ta có \(DM⊥NH;EN⊥NH\Rightarrow\)DM//EN
gọi giao điểm của DE và NH là T
xét tam giác vuông MTD và tam giác vuông NTE
góc MDT = góc NET ( so le trong )
DM = NE (cmt)
do đó \(\Delta MDT=\Delta NET\)(cạnh huyền góc nhọn )
suy ra DN = NE ( 2 cạnh tương ứng ) (1)
\(\Delta MDT\)và \(\Delta NET\)có \(\hept{\begin{cases}\widehat{MDT}=\widehat{NET}\\\widehat{DMT}=\widehat{ENT}=90^o\\\Rightarrow\widehat{DTM}=\widehat{ETN}\end{cases}}\)
ta có \(\widehat{NTE}+\widehat{MTE}=180^o\)( kề bù )
mà \(\widehat{NTE}=\widehat{DTM}\left(cmt\right)\)\(\Rightarrow\widehat{MTE}+\widehat{DTM}=180^o\)hay D;N;E thẳng hàng (2)
từ (1) và (2) suy ra N là trung điểm D;E
hay MN và AH đi qua trung điểm DE
câu c gửi bạn sau mk đi học r
chúc bạn học tốt

A B C H K E D F
c, có ^DAB = ^FAC = 90
^DAB + ^BAC = ^DAC
^FAC + ^BAC = ^FAB
=> ^DAC = ^FAB
xét tg DAC và tg BAF có : AD = AB (gt) và AF = AC (Gt)
=> tg DAC = tg BAF (C-g-c)
=> BF = DC (đn)

a: Xét ΔABD và ΔACD có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
=>BD=CD và góc ADB=góc ADC=180/2=90 độ
=>AD vuông góc bC
b: BD=CD=18/2=9cm
AD=căn 15^2-9^2=12cm
c: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
góc KBC=góc HCB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
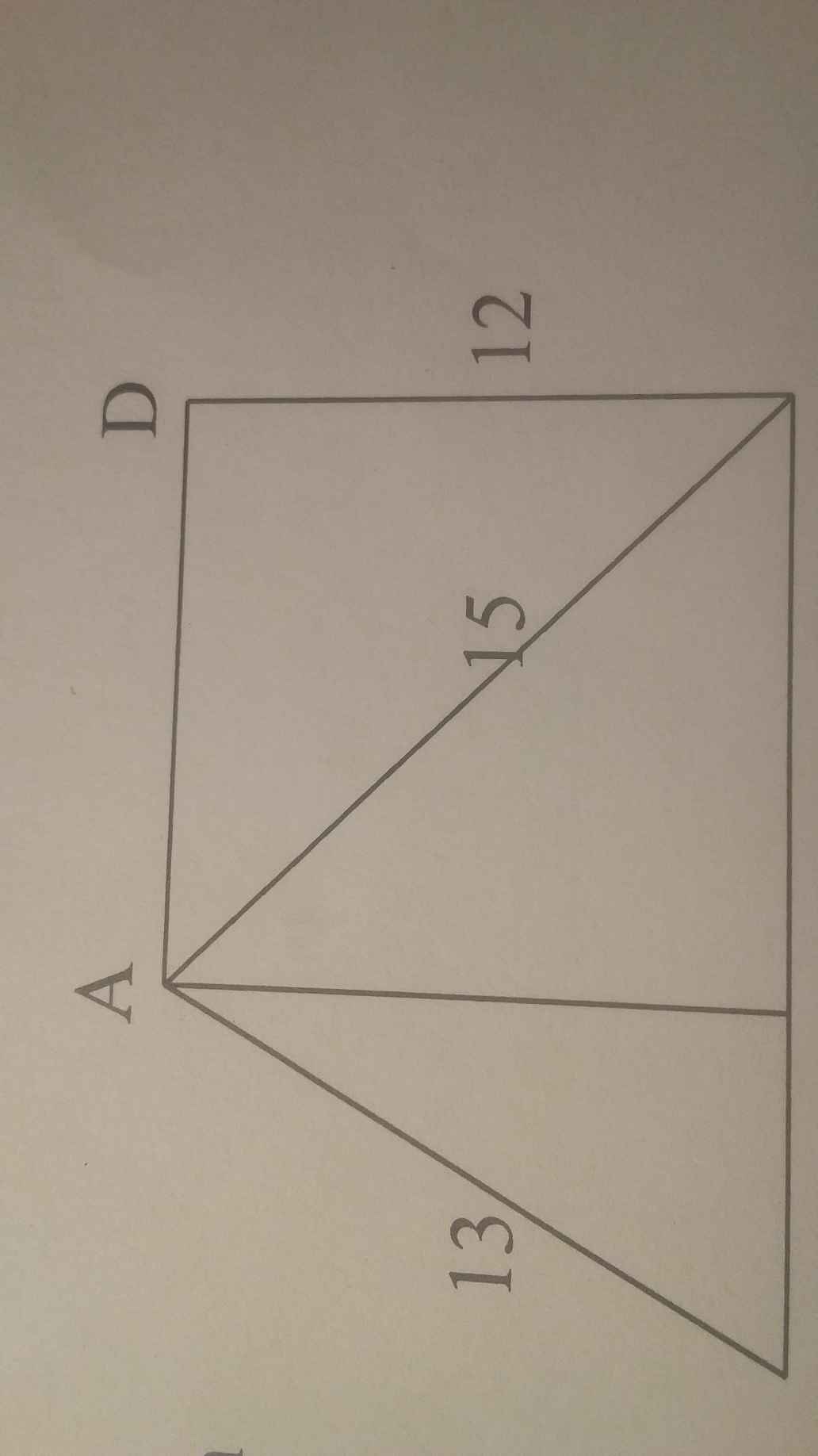


Xét tứ giác \(ADCH\) có:
\(\widehat{D}=\widehat{C}=\widehat{H}=90^o\)
\(\Rightarrow ADCH\) là hình chữ nhật
\(\Rightarrow AH=DC=12cm\)
Xét \(\Delta ADC\left(\widehat{D}=90^o\right)\) có:
\(AC^2=AD^2+DC^2\) (định lí pitago)
\(\Rightarrow AD=\sqrt{AC^2-DC^2}=\sqrt{15^2-12^2}=9cm=HC\)
Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) có:
\(AB^2=AH^2+BH^2\) (định lí pitago)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{13^2-12^2}=5cm\)
\(\Rightarrow BC=BH+HC=5+9=14cm\)
Vậy \(BC=14cm\)
Ảnh thiếu mấy điểm C, H