Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

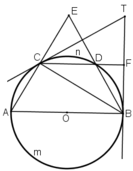
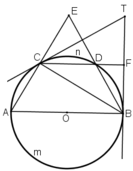
a) Ta có 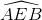 là góc có đỉnh ở bên ngoài đường tròn nên:
là góc có đỉnh ở bên ngoài đường tròn nên:
\(\widehat{AEB}=\dfrac{sđ\left(\widehat{AB}-\widehat{CD}\right)}{2}=\dfrac{180^O-60^O}{2}=60^O\)
và \(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:
\(\widehat{BTC}\) = sđ\(\dfrac{\widehat{BAC}-\widehat{BDC}}{2}=\dfrac{\left(180^O+60^O\right)-\left(60^O+60^O\right)}{2}=60^O\)
Vậy 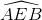 =
=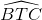
b) \(\widehat{DCT}\) là góc tạo bởi tiếp tuyến và dây cung nên:
\(\widehat{DCT}=\dfrac{sđ\widehat{CD}}{2}=\dfrac{60^o}{2}=30^o\)
→ \(\widehat{DCB}\) là góc nội tiếp trên
\(\widehat{DCB}\) = \(\dfrac{sđ\widehat{DB}}{2}\) = \(\dfrac{60^O}{2}=30^O\)
Vậy \(\widehat{DCT}\) = \(\widehat{DCB}\) hay CD là phân giác của \(\widehat{BCT}\)

a) + 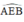 là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 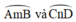
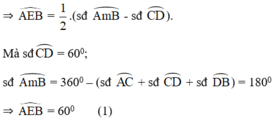
+  là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 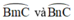

b)  là góc tạo bởi tiếp tuyến CT và dây CD
là góc tạo bởi tiếp tuyến CT và dây CD

Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

a) +  là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 
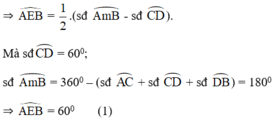
+  là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 


VE HINH
â) Xét tứ giác KCID ,co:
gocI = (cungAB+cungCD):2 = (180+60):2 = 120 độ
gocK=(cungAB-cungCD):2 =(180-60):2=60 độ
gócI+gocK=120do+60do=180 do
Vay : tứ giác KCID nội tiếp (tổng số đo 2 góc đối diện=180 độ )
:góc AKB = 60 độ
b)Ta có:AB//CD
=>cungAC=cungBD=(180-60):2=60 do (2 cung nằm giữa 2 dây song song thì = nhau )
=>AC=BD(2 dây chan 2 cung = nhau thi = nhau ) (1)
=>tứ giác ACDB là hình thang cân
***Xét : 3giac AKDva 3giac BKC ,co:
gocD=gocC=90do (vi gocC va gocD là góc nội tiếp chắn nửa đường tròn)
gocCAD=gocDBC(2goc noi tiep cung chan cungCD)
AD=BC(2 đường chéo của hình thang cân thì = nhau )(cmt)
Do do:3giacAKD =3giacBKC (g-c-g)
=>KD=KC (2 canh tương ứng) (2)
Ta lại có :KA=KC+AC(C nam giua A va K)
}(3)
:KB=KD+BD(D nam giua B va K)
Tu (1) ,(2) va (3) suy ra KA=KB (4)
Tu (2) va (4) suy ra KA.KC=KB.KD .
 là góc tạo bởi tiếp tuyến CT và dây CD
là góc tạo bởi tiếp tuyến CT và dây CD
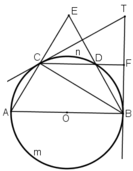
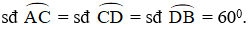 Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
a: Xét ΔOAC có OA=OC và góc AOC=60 độ
nên ΔOAC đều
=>góc CAO=60 độ
Xet ΔOBD có OB=OD và góc DOB=60 độ
nên ΔOBD đều
=>góc B=60 độ
Xét ΔEAB có góc EAB=góc EBA=60 độ
nên ΔEAB đều
=>góc E=60 độ
góc BOC=60+60=120 độ
=>góc BTC=60 độ=góc AEB